キルヒホッフ・ルース関数が、共形写像(conformal mapping)の下でどのように振る舞うかを考察するとしよう。今、$z$ 平面上の領域 $D$ 内で運動する $N$ 個の渦があり、その運動が複素ポテンシャル関数 $w(z)$ で記述されているとする。いま、この領域 $D$ を、共形写像 $z=Z(z’)$ によって、別の領域 $D’$ すなわち $z’$ 平面上に写像することを考える。
このとき、対応するポテンシャル関数は $w(z)\to w'(z’)$ に対応して、ここに $w’$ は $z’$ の解析関数であり、その境界上では $\Im\,w’ =(\mathrm{Im}\,w’) = 0$ であり、各渦の近傍では、$w’\sim \DL{ -\ff{\kappa_j}{2\pi} \log r_j’ }$ のような対数特異性を持つ。
領域 $D$ における渦系の運動は、キルヒホッフ・ルース関数 $\Psi (\B{z}), \B{z}=(z_1, z_2, \cdots, z_N)$ によって記述される。同様に、領域 $D’$ における運動はキルヒホッフ・ルース関数 $\Psi’ (\B{z}’)$ で記述される。ただし、一般に、これら二つの関数は単純な等価関係を持たない。すなわち、
$$
\begin{split}
\Psi(\B{z}) \neq \Psi'(\B{z}’)
\end{split} \qquad(1)
$$
である。このように、2つの領域における渦の軌跡は、共形写像 $Z$ によって単純に対応するわけではない。しかし、両者の間には一定の関係式が存在することに注意が必要である。つまり、$z-$平面上での渦の運動方程式は(式 7.3.7 の複素形)として、
$$
\begin{split}
u_j-iv_j = \ff{\diff \bar{z}_j}{\diff t} = \ff{\diff}{\diff z} \left[ w+\ff{i\kappa_j}{2\pi}\log(z-z_j) \right]_{z=z_j} = \ff{1}{\kappa}\left[ \ff{\del \Psi}{\del y_j}-i\ff{\del \Psi}{\del x_j} \right]
\end{split} \qquad(2)
$$
そして、
$$
\begin{split}
u_j’-iv_j’ = \ff{\diff \bar{z}_j’}{\diff t} = \ff{\diff}{\diff z’} \left[ w’+\ff{i\kappa_j}{2\pi}\log(z’-z’_j) \right]_{z’=z’_j} = \ff{1}{\kappa}\left[ \ff{\del \Psi’}{\del y’_j}-i\ff{\del \Psi’}{\del x’_j} \right]
\end{split} \qquad(3)
$$
となる。
さらに、連鎖律(第2章参照)より、
$$
\begin{split}
\ff{\diff \bar{z}_j}{\diff t} = \ff{\diff \bar{z}_j’}{\diff t} \ff{\diff z’}{\diff Z}+\ff{i\kappa_j}{4\pi} \ff{ \ff{\diff^2 Z}{\diff z’^2} }{ \left( \ff{\diff Z}{\diff z’} \right)^2 }
\end{split} \qquad(4)
$$
ここで、$Z$ の導関数は $z_j’$ で評価される。今、
$$
\begin{split}
\diff \Psi &= \sum_j \left( \ff{\del \Psi}{\del x_j}\diff x_j+\ff{\del \Psi}{\del y_j}\diff y_j \right) \EE
&= \Im\, \sum_j \kappa_j(u_j-iv_j)(\diff x_j+i\diff y_j) \EE
&= \Im\, \sum_j \kappa_j \ff{\diff \bar{z}_j}{\diff t} \diff z_j \EE
&= \Im \sum \kappa_j \ff{\diff \bar{z}_j’}{\diff t} \diff z_j’+\Im\, \sum_j \ff{i\kappa_j^2}{4\pi}\ff{\ff{\diff^2 Z}{\diff z’^2} }{ \ff{\diff Z}{\diff z’} } \diff z_j’ \EE
&= \diff \Psi’+\ff{1}{4\pi} \Im\, \sum_j i\kappa_j^2\,\diff \left( \log \ff{\diff Z}{\diff z’} \right)_{z_j’} \EE
&= \diff \Psi’+\ff{1}{4\pi}\sum_j \kappa_j^2\, \diff \left( \log \left| \ff{\diff Z}{\diff z’} \right|_{z’_j} \right) \qquad(5)
\end{split}
$$
したがって、
$$
\begin{split}
\Psi = \Psi’+\sum_{j=1}^N \ff{\kappa_j^2}{4\pi} \log \left| \ff{\diff Z}{\diff z’} \right|_{z’_j}
\end{split} \qquad(6)
$$
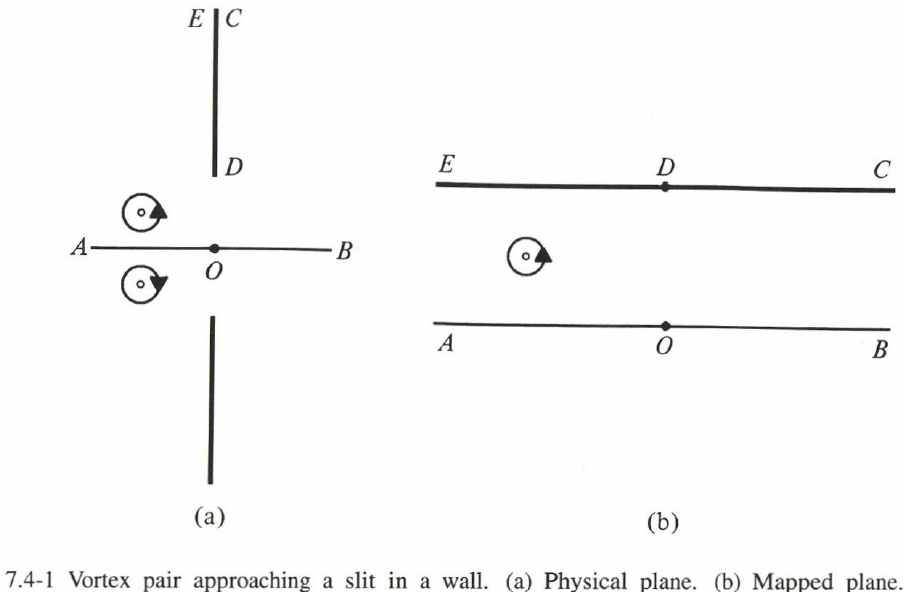
経路関数の応用例として、対称的に配置された、強度 $\kappa$ の逆回転する渦対が壁のスリットに垂直に接近する運動を考えよう(Karweit [975])。図7.4-1を参照。等角写像 $z=\sinh\zeta, z=x+iy, \zeta=\xi+i\eta$ は、上半平面を $\zeta$平面上の幅 $\pi/2$ の帯に写す。チャネル内の渦によって誘起される複素ポテンシャルは第2章で与えている。つまり、
$$
\begin{split}
w &= -\ff{i\kappa}{2\pi}\log \left( \sinh \ff{\zeta-\zeta_0}{\zeta-\bar{\zeta_0}} \right) \EE
&= -\ff{i\kappa}{2\pi} \log \left( \ff{ z\sqrt{1+z_0^2}-z_0\sqrt{1+z^2} }{ z\sqrt{1+\bar{z_0}^2}-\bar{z_0}\sqrt{1-z^2} } \right) \qquad(7)
\end{split}
$$
となる。
ここで、$z_0$ は上半平面における渦の位置である。軌道を求めるには、まず $\zeta$ 平面における経路関数を求める必要がある。第2章の結果から、渦の速度は、
$$
\begin{split}
u_0′ = -\ff{\kappa}{2\pi \tan 2\eta_0} = \ff{1}{\kappa} \ff{\del \Psi’}{\del \eta_0} \qquad(8)
\end{split}
$$
と表せて、したがって、経路関数 $\Psi’$ は
$$
\begin{split}
\Psi’ = \ff{\kappa^2}{4\pi} \log(\sin 2\eta) \qquad(9)
\end{split}
$$
となる。今、$\DL{ \ff{\diff z}{\diff \zeta} = \cosh \zeta}$ とおくことにする。そして、元の平面における経路関数は、このようになる。
$$
\begin{split}
\Psi = \ff{\kappa^2}{4\pi} \log(\sin 2\eta)+\ff{\kappa^2}{4\pi} \log \big (\cosh^2\xi-\sin^2\eta \big)^{1/2} \qquad(10)
\end{split}
$$
図7.4-2に、$\Psi = const.$ の軌道を描いている。この軌跡は $\tan \eta=1/\sqrt{3}$ のときに生じる分割軌道 $\DL{\ff{\del \Psi}{\del \eta} = 0}$ 上のものである。したがって、分割流線の方程式は、
$$
\begin{split}
\sin 2\eta (\cosh^2\xi-\sin^2\eta \big)^{1/2} = \ff{4}{3\sqrt{3}} \qquad(11)
\end{split}
$$
となる。
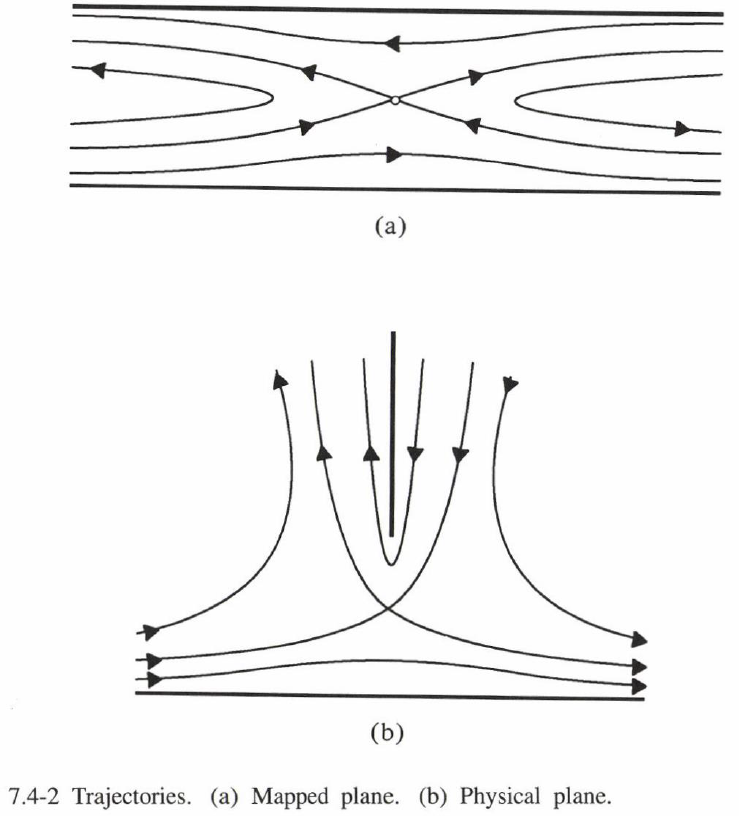
式(11)より、無限遠から来る流線対は、間隔が $\DL{ \ff{4}{3\sqrt{3}} }$ 未満であれば幅 $2$ のスリットを通過することが容易に分かる。そうでなければ、流線対は反射される。
得られた解にはいくつかの問題点がある。例えばクッタ条件が破れているため、スリットの縁から渦層が放出される流れを研究するのが適切であると考えられる。また、スリットを横切る圧力の急上昇も存在している。式(7)から、無限遠漸近線における速度ポテンシャルは、
$$
\left\{
\begin{split}
\phi(+\infty) &= -\ff{\kappa}{2\pi} i\big( \bar{\zeta_0}-\zeta_0 \big) = -\ff{\eta_0}{\pi} \qquad(12) \EE
\phi(-\infty) &= -\ff{\kappa}{2\pi} i\big( \zeta_0-\bar{\zeta_0} \big) = \ff{\eta_0}{\pi} \qquad\,\,\,\,\,(13)
\end{split}
\right.
$$
となる。
非定常ベルヌーイ方程式から、$\eta_0$ は $t$ に依存する場合(=渦位置が時間とともに変化する場合)、
$$
\begin{split}
p(+\infty) \neq p(-\infty) \qquad(14)
\end{split}
$$
であることが言え、要するに、圧力差が残る非一様な流れとなる。
ただし、この解は一意ではない。なぜなら、$w_Q = Q\zeta = Q\sinh^{-1}z $($Q$ は実数) のような付加的ポテンシャル項を(7)に加えることができるからである。これは、スリットを通過する流速 $Q\pi$ に対応する。
このとき、$Q$ を適切に選べば、Kutta条件(端点での速度有限条件)を満たすことができる。例えば、$\zeta = i\pi/2$ において $\DL{ \ff{\diff w}{\diff \zeta}-Q=0 }$ となるように、$Q = -\DL{\ff{\kappa}{2\pi}\sin \ff{2\eta_0}{\cos 2\eta_0-\cosh 2\xi_0 } }$ とすればよい。ただし、$Q=Q(t)$ は無限大にて圧力が発散する。
他の解として、スリット端に多重極(multipole)特異性を加えることも可能である。例えば、
$$
\begin{split}
w_m = \ff{m}{(1+e^{2\zeta})^n}\quad(n=1,2,\cdots) \qquad(15)
\end{split}
$$
のような項を追加できる。この場合、流れ関数 $\psi_m$ はスリット上 $\eta = 0, \pi/2$ で消失するが、(15)式を加えても Kutta 条件そのものは依然として満たされない。しかし、速度ポテンシャル $\phi_m$ については以下を満たす。
$$
\begin{split}
\phi_m(\infty) = 0, \quad \phi_m(-\infty) = m \qquad(16)
\end{split}
$$
さらに、$m = \DL{ -\ff{2\eta_0}{\pi} }$ と選べば $p(+\infty) = p(-\infty)$ となって、圧力の不連続は消える。このような修正を施すと、ポテンシャル関数を単純に用いて軌跡を求めることはできないが、より物理的に整合した流れの解を構成できる。

コメント