Kelvin [1867b](Tait [1867] による Helmholtz [1858] の論文訳への付記) は、循環 $\G$ で渦輪半径 $R$、コア半径 $a$ の薄いコア $a/R\ll1$ の渦輪の移動速度 $U$ について、説明なしに次式を与えている。
$$
\begin{split}
U = \ff{\G}{4\pi R} \left[ \log\ff{8R}{a}-\ff{1}{4} \right]
\end{split} \qquad(1)
$$
Hicks [1885] は一様渦度の薄い渦輪について Kelvin の結果を確認している。また、空洞(hollow)あるいは停滞(stagnant)している薄い渦輪の速度として以下を与えている。
$$
\begin{split}
U = \ff{\G}{4\pi R} \left[ \log\ff{8R}{a}-\ff{1}{2} \right]
\end{split} \qquad(2)
$$
Dyson [1970] は一様渦輪の速度を、誤差 $\DL{ O\left( \ff{\G a^4}{R^5 \log\ff{8R}{a}} \right) }$ のオーダーで求めており、そして境界形状の変形の誤差を $\DL{ O\left( \ff{a^4}{R^4 \log\ff{R}{a}} \right) }$ のオーダーで求めている。

Fraenkel [1970] は、(スワール無しの)一般の $F(Ppsi)$ に対し、$\eps$ での体系的展開法を記述している。手法の要点は次のとおりである。まず、定常運動の座標系で、領域 $A$ の内部によどみ点 $O$ をとる。$\Psi$ は $\del A$ 上で一定なので、最小値を少なくとも 1 つ持つが、そこがよどみ点である(図 10.2–1)。次に、原点 $O$ を中心とする座標系 $x=r\cos\q, y=r\sin\q+l$ をとる。そして、以下の未知の写像、
$$
\begin{split}
r = s+q(s,\q,a) \quad(0 \leq s \leq a)
\end{split} \qquad(3)
$$
について考える。ここに、$s=const.$ の曲線が $\Psi=const.$ に写像されるという性質を持つ。また、境界 $\del A$ は $s=a$ に相当する。
今、$\om = \DL{\ff{y}{l}\Omega(s) }$ と与えられていると仮定しよう、つまり、$\Omega(s)$ は既知($s>a$ で $0$ ただし、一般に $\Omega(a) \neq 0$)であって、さらに、定常流における流線上の渦度の値を規定する $F(\Psi)$ と同値と見なせる。これを(1.11)に代入すると以下の積分微分方程式が得られる。($G$ は第1節で定義した流れ関数)
$$
\begin{split}
\Psi(s) = -\ff{1}{2}Uy^2+\int_0^a\int_0^{2\pi} (s’+q’)\left( 1+\ff{\del q’}{\del s’} \right)\ff{y’\Omega’}{l}\, G(x-x’,y,y’)\diff s’\diff \q’
\end{split} \qquad(4)
$$
上式におけるプライム($’$)は $0\leq s\leq a,\, 0\leq \q \leq 2\pi$ の $r’, \q’$ における評価を表している。この方程式は $\eps = \DL{\ff{a}{l}}$ について $\DL{\ff{q}{s}\to0}$ のときに $\eps\to0$ となることを利用して、$\eps$ で逐次展開することで解くことができる。
後に説明する式(9)を用いることで、Fraenkel は(4)から以下の結果を得ている。
$$
\begin{split}
U = \ff{\G}{4\pi \overline{R}} \left[ \log \ff{8\overline{R}}{a}-\ff{1}{2}+2\pi^2a^2 \overline{V^2} \right]\left\{1+O\left[ \left( \ff{a}{\overline{R}} \right)^2\log \ff{\overline{R}}{a} \right] \right\}
\end{split} \qquad(5)
$$
なお、$V$ と $\overline{V^2}$ はこのように定義される。
$$
\left\{
\begin{split}
&\, \ff{1}{s}\ff{\diff (Vs)}{\diff s} = \Omega(s) \\[8pt]
&\, \overline{V^2} = \ff{2}{a^2} \int_0^a sV^2\diff s
\end{split} \qquad(6)
\right.
$$
$V$ は、単一の直線円渦のコア周りの接線速度であり、$\overline{R}$ と $\G$ は、コア周りの重心の半径と全循環である。この結果にはケルビンの結果も含まれており、このようになる。
$$
\left\{
\begin{split}
&\, \Omega = \ff{\G}{\pi a^2} \EE
&\, V = \ff{\G s}{2\pi a^2} \EE
&\, \overline{V^2} = \ff{\G^2}{8\pi^2 a^2}
\end{split} \qquad(7)
\right.
$$
Hicks は、$V=0$ として、式(6)を積分した結果は $0$ となることを述べている。
一様なコア(つまり、$\Omega=const.$ )のときは、直接計算することができる。すなわち、完全楕円積分の漸近的性質から以下が得られる。($k’$ は補完係数と呼ばれ、$k’^2 = 1-k^2$ の関係にある)
$$
\begin{split}
\left( \ff{2}{k}-k \right)K(k)-\ff{2}{k}E(k)\sim \log \ff{4}{k’}-2+O(k’^2\log k’)
\end{split} \qquad(8)
$$
さて、$x=r\cos\q, y=\ovr+r\sin\q$ を $G$ に代入して、いくつかの代数計算を実行すると、下が得られる。
$$
\begin{split}
G = \ff{\ovr}{2\pi}\left\{ \log \left( \ff{8\ovr}{\sqrt{ r^2+r’^2-2rr’\cos(\q-\q’) }} \right) \left[ 1+\ff{r\sin\q+r’\sin\q’}{2\ovr} \right]-2-\ff{r\sin\q+r’\sin\q’}{2\ovr}+O\left(\ff{r^2}{\ovr^2}\log \ff{\ovr}{r} \right) \right\}
\end{split} \qquad(9)
$$
さて、流れ関数を評価するには、渦度の分布の情報が不可欠となる。しかしながら、一般的なコア構造の場合、これは困難であり、Fraenkel の手順、あるいはそれと同等の手順が必要となる。ただし、均一なコアの場合、次が成立することが知られている。
$$
\begin{split}
\om = \ff{\om_0 y}{\ovr} = \om_0 \left( 1+\ff{r\sin\q}{\ovr} \right)
\end{split} \qquad(10)
$$
問題は形状である。本来は半径を $\q$ のフーリエ級数として展開すべきだが、簡潔にするために結果を先回りして、境界は1次まで円形であると仮定する。つまり、$r=\DL{ a\left\{ 1+O\left( \ff{a^2}{\ovr^2}\log \ff{\ovr}{a} \right) \right\} }$ の形であると想定する。面積 $\diff x \diff y$ の要素が $\DL{ \left( 1+\ff{s}{\ovr}\sin\q \right) } r\,\diff r\,\diff \q$であることを思い出すと、以下が得られる。
$$
\begin{split}
\psi(r,\q) &= \ff{\ovr\om_0}{2\pi} \int_0^a\int_0^{2\pi} \left\{ \log \ff{8\ovr}{\sqrt{r^2+r’^2-2rr’\cos(\q-\q’)}} \right. \EE
&\quad \left. \times \left[ 1+\ff{r\sin\q+3r’\sin\q’}{2\ovr} \right]-2-\ff{r\sin\q+5r’\sin\q’}{2\ovr} \right\}r’\diff r’\diff \q’
\end{split} \qquad(11)
$$
この積分を評価するために、以下の結果を用いる。
$$
\int_0^{2\pi} \log \sqrt{r^2+r’^2-2rr’\cos(\q-\q’)}\,\diff \q’ = \left\{
\begin{split}
&\, 2\pi \log r’ \qquad(r’>r) \EE
&\, 2\pi \log r \qquad\,\,(r>r’)
\end{split}
\right.
$$
$$
\int_0^{2\pi} \cos(\q-\q’) \log \sqrt{r^2+r’^2-2rr’\cos(\q-\q’)}\,\diff \q’ = \left\{
\begin{split}
&\, -\ff{\pi r}{r’} \qquad\,\,(r’>r) \EE
&\, -\ff{\pi r’}{r} \qquad(r>r’)
\end{split}
\right.
$$
これにより(11)を積分することができ、$\G = \pi a^2 \om_0$(これはコアを通る渦度のフラックス)を定義すると、$0 \leq r \leq a$(コアは円形と仮定)に対して以下が得られる。
$$
\begin{split}
\psi(r,\q) &= \ff{\G \ovr}{2\pi}\left\{ \log\ff{8\ovr}{a}-\ff{3}{2}-\ff{r^2}{2a^2}+\ff{r\sin\q}{2\ovr}\left[ \log\ff{8\ovr}{a}+1-\ff{5r^2}{4a^2} \right]+O\left( \ff{a^2}{\ovr^2}\log\ff{\ovr}{a} \right) \right\}
\end{split} \qquad(12)
$$
$G$ の近似を行う時、(12)を $\DL{O\left( \ff{a}{R} \right)}$ のオーダーに一致させるためには不十分である。まず、渦固定座標系では、
$$
\begin{split}
\Psi = -\ff{1}{2}Uy^2+\psi, \qquad y^2=\ovr^2 \left( 1+\ff{2r}{\ovr}\sin\q+O\left( \ff{a^2}{\ovr^2} \right) \right)
\end{split} \qquad(13)
$$
である。
したがって、$\DL{r=a\left(1+O\left( \ff{a^2}{\ovr}^2\log \ff{\ovr}{a} \right) \right)}$ 上にて $\Psi=const.$(コアが円形であることを確認せよ)であることが分かる、もし(12)式の $\sin\q$ の係数が $Ua\ovr$ に等しい場合、ケルビンの式(1)を与えるとその誤差は、$\DL{ O\left( \ff{\G a^2}{\ovr^3} \log \ff{\ovr}{a} \right) }$ のオーダーとなる。
渦固定座標系におけるコア内部の流線は、$r=r_0+\eta(\q),$ $(\eta \ll r_0 ,\, 0\leq r_0 \leq a)$ で与えられる。$U$ の値を $\Psi$ の式に代入すると、$r\leq a$ にて以下を得る。
$$
\begin{split}
\Psi = \ff{\G \ovr}{2\pi} \left\{ \ff{3}{4}\log \ff{\ovr}{a}-\ff{23}{16}-\ff{r^2}{2a^2} \right\}+\ff{\G r\sin\q}{4\pi}\left\{ \ff{5}{4}-\ff{5r^2}{4a^2} \right\}+O\left( \ff{a}{\ovr} \right)
\end{split} \qquad(14)
$$
以上より、流線の方程式 $\Psi = const.$ はこのようになる。
$$
\begin{split}
\ff{r^2}{a^2} = \ff{5t}{4\ovr} \sin\q \left( 1-\ff{r^2}{a^2} \right)+\ff{r_0^2}{a^2}
\end{split}
$$
整理すると、
$$
\begin{split}
r = r_0+\ff{5}{8}\left( \ff{a^2-r_0^2}{\ovr} \right)\sin\q \qquad(0\leq r_0 \leq a)
\end{split} \qquad(15)
$$
となる。
これらの曲線は、境界の中心から $\DL{\ff{5(a^2-r_0^2)}{8\ovr}}$ の距離だけ上にある非同心円の族を構成する。そして、よどみ点($r_0=0$)は軸から $\ovr+\DL{\ff{5a^2}{8\ovr}}$ の距離にある。
Dyson によって導かれた高次近似の式(Fraenkel [1972]も参照)は、前節の最後で定義した $R$ と $\eps$ を用いて表すことができる。その速度はこのようになる。
$$
\begin{split}
U = \ff{\G}{4\pi R}\left\{ \log\ff{8}{\eps}-\ff{1}{4}+\eps^2\left[-\ff{3}{8}\log\ff{8}{\eps}+\ff{15}{32} \right]+O\left( \eps^4\log\ff{8}{\eps} \right) \right\}
\end{split} \qquad(16)
$$
さらに、$(R, 0)$ を中心とする極座標におけるコアの形状はこのようになる。
$$
\begin{split}
r &= \eps R\left[ 1-\eps^2\left\{ \ff{3}{8}\log\ff{8}{\eps}-\ff{17}{32} \right\}\sin2\q \right. \EE
&\left.\quad-\eps^3\left\{ \ff{21}{128}\log\ff{8}{\eps}-\ff{273}{1024} \right\}(\sin\q+\sin3\q)+\cdots \right]
\end{split} \qquad(17)
$$
このとき、コアの先導次数(leading order)の変形は楕円であり、その長短軸比は
$$
\begin{split}
1+\eps^2\left\{ \ff{3}{8}\log\ff{8}{\eps}-\ff{17}{32} \right\}
\end{split} \qquad(18)
$$
で表され、軸に平行な方向に扁平化する。なお、コア内のよどみ点は(コアの前後対称性から直ちに)$\q =0$ の点にあると言えて、その位置はこのようになる。
$$
\begin{split}
r = \ff{5}{8}\eps^2+\eps^3\left[-\ff{99}{128}\log \ff{8}{\eps}+\ff{739}{1024} \right]
\end{split} \qquad(19)
$$
運動エネルギー $E$ と流体力学的インパルス $\B{I}$(軸に平行な成分のみがゼロではない)は、それぞれ 3.11.7 と 3.2.8 から計算でき、以下のように与えられる。
$$
\begin{split}
E = \pi \int \om \psi \,\diff x\,\diff y = \ff{\G^2 R}{2}\left\{ \log\ff{8}{\eps}-\ff{7}{4}+\ff{3}{16}\eps^2\log\ff{8}{\eps}+\cdots\right\}
\end{split} \qquad(20)
$$
$$
\begin{split}
I = \pi \int \om y^2\,\diff x\,\diff y = \pi R^2\G \left\{ 1+\ff{3}{4}\eps^2+\cdots \right\}
\end{split} \qquad(21)
$$
例えば、ヒルの球形渦を例にすると各パラメータは、$\DL{ R=\ff{1}{2}a, U=\ff{\G}{10R}, I=2\pi a^3U, E=\ff{10}{7}\pi a^3 U^2 }$、無次元パラメータは、$\DL{ \ff{UR}{\G}=0.1, \ff{E}{\G^2 R}=0.359, \ff{I}{R^2\G}=5.027 }$ となる。また、$\eps=\sqrt{2}$ を上の公式達に適用すると、各値は $0.089, 0.316, 7.85$ となる。なお、Norbury [1973] は、$\eps$ の関数として、均一で太い渦輪の特性を数値的に計算している。
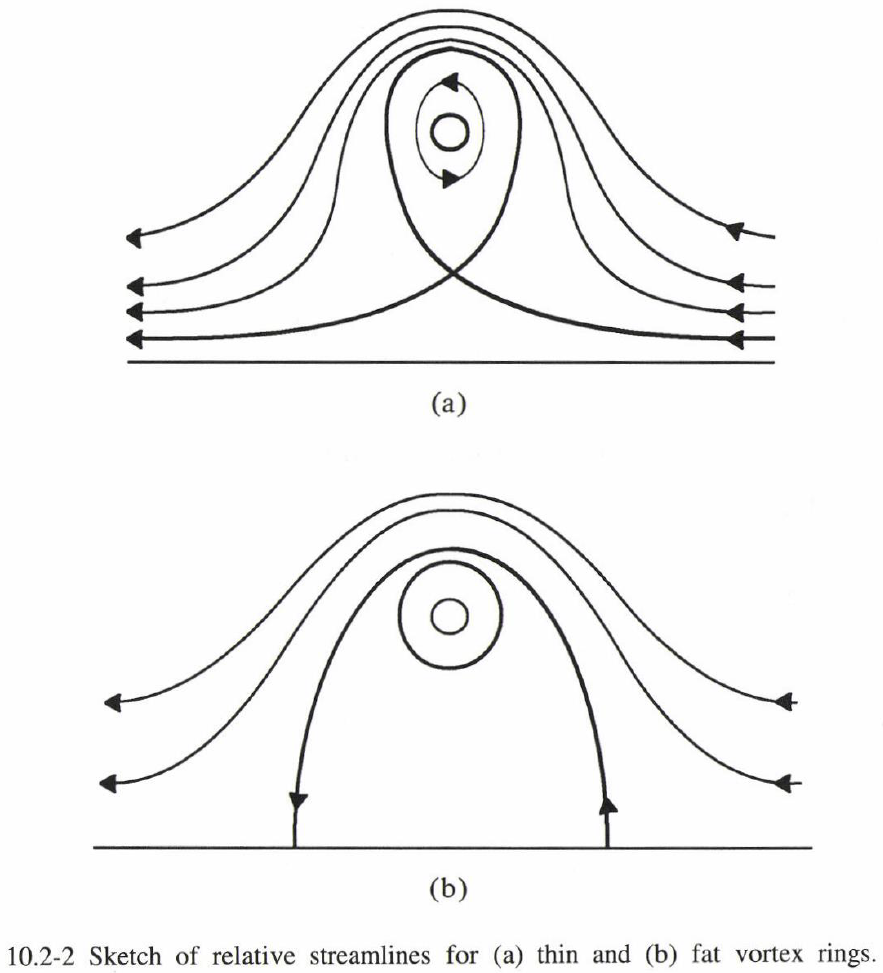
興味深いのは、渦輪によって運ばれる非回転流体の体積である。渦輪によって共に運ばれる無回転流体の体積は、コア外側の外部よどみ点(渦と共に移動する座標系にて)を含む流線によって囲まれる体積である。薄い渦輪(図 10.2–2a)では軸上に 2 点の外部よどみ点があり、渦と共に動く流体の形は閉じた楕円になる。他方、太い渦輪(図 10.2–2b)では、コアと軸の間に1点の外部よどみ点しかなく、渦と共に動く流体の形は輪状になる(図 10.2–2参照)。
これらの切り替わりが生じるコア半径の概算は、Biot–Savart 則から計算できる。軸上 $y=0$ において、渦輪を円形フィラメントで近似したときの速度は $\DL{ \ff{\G R^2}{2(x^2+R^2)^{3/2} } }$ で与えられる。したがって、薄い芯のあるリングの渦固定座標において $x$ が次式を満たすとき、よどみ点が存在する。
$$
\begin{split}
\ff{\G R^2}{2(x^2+R^2)^{3/2}} = \ff{\G}{4\pi R}\left( \log\ff{8R}{a_e}-\ff{1}{4} \right)
\end{split} \qquad(22)
$$
ここで、均一な渦輪の場合は $a_e=a$、中空ないしは停滞した渦輪の場合は $a_e=ae^{1/4}$ そして、$a_e$ は次節の公式を用いて、一般的な分布のコア構造によって表すことができる。なお、この方程式は $a_e/R < 1/86$ の場合には解が存在しない。またこの場合、渦輪の中心にある流体は渦輪と共には移動しない。

コメント