渦度が無限大の面は、運動学的に存在可能であり、必ずしも運動学的原理には違反しない。それらは、速度場の接線成分が不連続である面を与え、渦層と呼ばれる。それらは、不連続の面として形式的に導入することも、渦度と渦線が、厚さ $\eps$ の薄い面状の領域に閉じ込められた、極限的な状態と考えることもできる。すなわち、$\eps\to 0$ の極限で、渦度の大きさが $\eps \omega\to \kappa$($\kappa$ は有限)となるようにして、そして、面上の位置についての関数となる。
渦度はベクトルであるため、大きさ(渦度の強さ)と向きを持つ。渦層内の渦度は、以下の形式で表すことができる。
\begin{split}
\B{\om} = \B{\kappa} \delta(n) \qquad(1)
\end{split}
ここに、$\delta(n)$ はディラックのデルタ関数、$\B{\kappa}\cdot\B{n}=0,\,n=|\B{n}|$ であり、$\B{n}$ は渦層に対する法線ベクトル、$\B{\kappa}$ は渦層に平行な曲線として定義する。また、渦度のソレノイダル性より、
\begin{split}
\text{div}\,\B{\kappa} = 0 \qquad(2)
\end{split}
が言える。なお、この発散は面上で二次元である。式(2)の帰結として、渦層は閉じているか境界上で終わることが言える。
渦層は、渦無し流れの流体領域を分離している。そのため、渦線は渦層内の領域に閉じ込められていると暗黙のうちに仮定されている。ただし、この制限は厳密には必要では無い。渦層は、渦層に隣接する滑らかな渦度がある場合にも定義できる。
この場合、流体中の渦線は、渦層に平行であったり、交差したりすることがある。例えば、回転軸に垂直な一様な渦線により貫かれる、剛体回転している流体に渦層を配置できる。渦線が交差する場合の動力学は、興味深い一連の問題を生じる。このとき、些細ではない変化が生じ、式(1)は修正を余儀なくされ、式(2)はもはや成り立たなくなる。結果を示すと、(2)は次式に取って代わられる。
\begin{split}
\text{div}\,\B{\kappa} = \big[ \B{\omega}\cdot \B{n} \big]_2^1 \qquad(3)
\end{split}
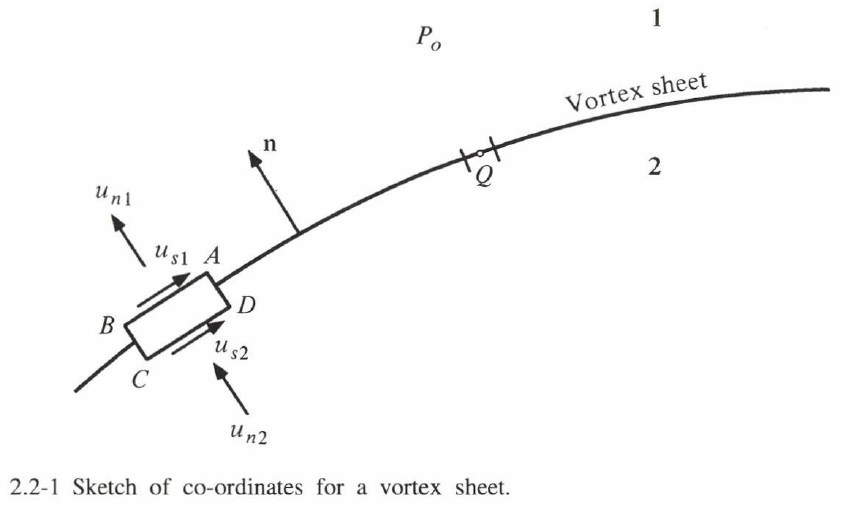
ここに、$[\,f\,]_2^1$ は、領域 $1$ から $2$ への跳躍、すなわち領域 $1$ の値から $2$ の値を引いたものを表すと約束する。(イメージ図については、図2.2-1 を参照のこと)渦層の線は、層内に始まって層内で終わる可能性がある。実際、渦層が線渦により仕切られているまたは、縁取られていると考えることはしばしば有用である。
なお、回転流における渦層の性質についての研究はほとんど行われていないようで、一様せん断流中の、渦層のケルビン・ヘルムホルツ不安定性を研究した Kiya と Arie を除いてほとんど例がない。
さて、渦層により誘導される速度 $\B{u}_v$ は、式(1.1.5)より求められる。式(1)をこの式に適用することを考える。渦層の面上 $S_v$ においては体積積分が面積分になることに注意すると、次式が得られる。
\begin{split}
\B{u}_{\text{v}}&=\ff{1}{4\pi}\int_{S_v} \ff{\B{\kappa}(\B{S},t)\times (\B{x}-\B{S})}{|\B{x}-\B{S}|^3} \,\diff S \qquad(4)
\end{split}
ここに、$\B{S}$ は面上の位置ベクトルで、$\diff S$ は微小面積要素である。式(4)で定義される速度は、考えている場の点 $\B{x}$ が渦層から離れているときには有限である。
今、位置ベクトルが $\B{x}$ である点 $P$ を、渦層上の点 $Q$ に近づけていく場合の挙動について考えよう。これを考えるに当たり、式(4)を以下のように書き換える。
\begin{split}
\B{u}_{\text{v}}(P) &=\ff{\B{\kappa}(Q)}{4\pi}\times \int_{S_v} \ff{\B{r}_{PS}}{r^3_{PS}} \,\diff S+\ff{1}{4\pi}\int_{S_v} (\B{\kappa}(S)-\B{\kappa}(Q))\times \ff{\B{r}_{PS}}{r^3_{PS}} \diff S \qquad(5)
\end{split}
標準的な解析過程から、右辺第二項は、$P\to Q$ のときに唯一の極限値を持つことが示される。第一項の極限は有限だが不連続であり、渦層への近づき方により値がことなる。すなわち、以下のような差がある。
\begin{split}
\lim_{P_1\to Q} \ff{\B{\kappa}(Q)}{4\pi}\times \int_{S_v} \ff{\B{r}_{PS}}{r^3_{PS}} \,\diff S-\lim_{P_2\to Q} \ff{\B{\kappa}(Q)}{4\pi}\times \int_{S_v} \ff{\B{r}_{PS}}{r^3_{PS}} \,\diff S=4\pi \B{n}(Q) \qquad(6)
\end{split}
ここに、$\B{n}$ は、領域 2 から 1 へ向かう方向であるとする。この結果は、次の形式にまとめられる。
\begin{split}
\lim_{P\to Q}\,\B{u}_v(P)=\pm \ff{1}{2}\B{\kappa}(Q)\times \B{n}(Q)+\B{q}_v(Q) \qquad(7)
\end{split}
ここに、
\begin{split}
\B{q}_v(Q)=\ff{1}{4\pi}\int \B{\kappa}(S)\times \ff{\B{x}(Q)-\B{x}(S)}{|\B{x}(Q)-\B{x}(S)|^3}\diff S \qquad(8)
\end{split}
であるとする。この計算は、コーシーの主値積分に類似した形式を持っており、$Q$ を中心とする無限小円内の渦度は積分から除外されている。式(7)の符号は、$P$ が $\B{n}$ が指す方向側から近づく場合には正である。また、$\B{q}_v$ は2つの極限の算術平均でもある。
ゆえに、渦層により生成される速度は有限であるが、渦層上の接線成分で単純な跳躍を持ち、法線成分は連続である。接線成分の跳躍 $[\B{u}]_2^1$ は、
\begin{split}
\big[ \B{u} \big]_2^1 = \B{\kappa}\times\B{n} \qquad(9)
\end{split}
となる。これらの結果は、有限な速度が与えられた場合、無限小の検査領域と長方形の考察から簡単に導くことができる。記法の説明については、図2.2-1を参照。検査領域の側面を通る質量保存則は、法線速度が連続あることを意味して、ゆえに $\B{u}_{n1}=\B{u}_{n2}$ となる。
長方形 $ABCD$ 周りに循環は $AB\times (u_{s2}-u_{s1})$ であり、これは閉曲線を貫く渦速度 $\kappa AB \sin\q$ に等しい。ここに、$\q$ は閉曲線が成す平面と、渦度方向の間の角度とする。よって、
$$
\left\{
\begin{split}
\, &\big[ \B{u} \big]_2^1 = \B{\kappa}\times\B{n} \,\,\,\text{ないしは,} \EE
\, &\B{\kappa} = \B{n}\times \big[ \B{u} \big]_2^1
\end{split}
\right. \qquad(10)
$$
となる。速度場の完全な決定には、積分(8)の評価と他の渦度分布および境界からの寄与の追加が必要である。
渦層を特異分布の渦度(=式(1))として導入するのではなく、速度の不連続面として導入する場合、その強さは式(10)で与えられる。実際の粘性流体では、渦層は粘性の作用で拡散して広がるので、せいぜいが初期の瞬間にしか存在できないが、粘性が小さな流体では貴重な理想化を提供する。
渦層により誘導される速度の別表現は、等価な双極子の面分布の考察から与えられる。渦層は、非回転運動の流体領域を分離しているとして、$\phi_1$ と $\phi_2$ を渦層上の点 $Q$ を挟んで対向する速度ポテンシャルであるとしよう。すると、このようになる。
\begin{split}
\phi_2-\phi_1 = \int^Q \big[ \B{u} \big]_1^2\cdot\,\diff \B{s} = \int^Q \B{n}\times \B{\kappa}\cdot\,\diff \B{s} \qquad(11)
\end{split}
これは、渦層上のある基準点(たとえば原点)から $Q$ への経路には依存しない、それゆえ固有な値となる。ただし、渦層上の全ての経路が縮約可能であることが条件である。そうでない場合(渦層がトーラスのような形をしているなど)、領域に仕切りを入れて経路が縮約可能になるようにして、これらの障壁(速度ポテンシャルが不連続である場所)が渦層の一部とみなされるようにする。
ところで、渦層から離れた点での速度ポテンシャルはこのように記述される。
\begin{split}
\phi(\B{x},t) = -\ff{1}{4\pi}\int_{S_v} \big[ \phi(\B{x}’) \big]_1^2 \B{n}’\cdot\, \ff{\B{x}-\B{x}’}{|\B{x}-\B{x}’|^3} \diff S’\qquad(12)
\end{split}
これは、強度密度が $\DL{ \ff{ \B{n}(\phi_2-\phi_1) }{4\pi} }$ の双極子が面分布している場合のポテンシャルである。式(12)で定義される $\phi$ は、渦層を横切って $\phi_2-\phi_1$ の跳躍を持ち、$\DL{\ff{\del \phi}{\del n}}$ が連続であることが示される。ゆえに、(12)の勾配で与えられる速度場は、渦層によるものと言える。 式(11)を(12)に代入し、適切に障壁を導入して勾配を取ると、速度場の式(5)が得られることも直接示せる。
これまでの議論は完全に運動学的であった。今度は、渦層の動力学とその運動について考えよう。流体が非粘性かつ保存力の影響下にあるとき、渦線は流体と共に移動する。そのため、渦層も流体と共に移動し、渦層を構成する流体粒子も同じままであると期待できる。
したがって、渦層の法線方向速度は、流体の速度に等しいと考えられる。この推論は、(実験的に)正しいことが知られているが、ヘルムホルツの法則の証明が、渦層を与える極限過程と交換可能であると仮定しているため、その論証は不適切である。
また、ケルビンの循環定理の証明の代替的なアプローチは、速度が連続であることに依拠しているので、渦層の存在下では、不十分な議論となる。
速度跳躍の存在は、オイラー方程式(式(1.5.2))の積分形式を用いることを余儀なくされる。この方程式を検査体積 $V$ 上で積分すると、以下を得る。
\begin{split}
\ff{\del}{\del t}\int_V\B{u}\diff V = -\int_{\del V}\big[ p\diff \B{S}+\B{u}(\B{u}\cdot \diff \B{S}) \big]+\int_V\B{F}\,\diff V \qquad(13)
\end{split}
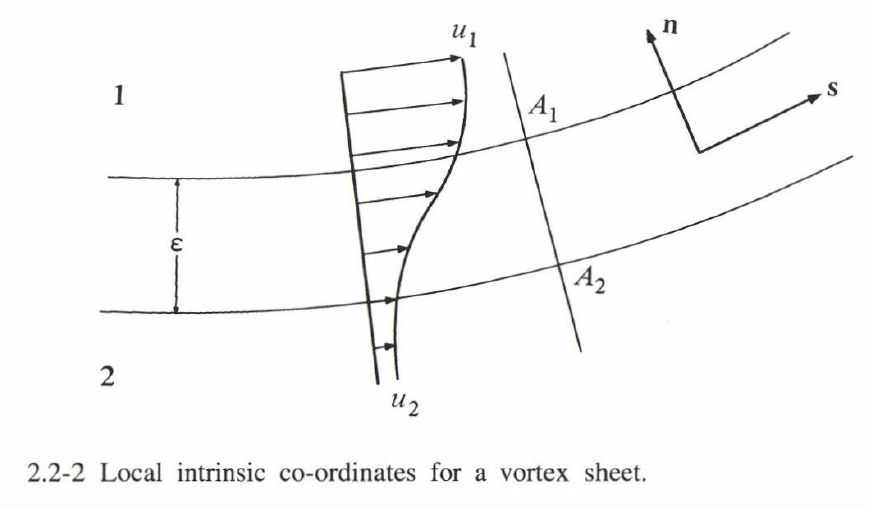
体積として、図2.2-2 の無限小な検査体積を考えよう。また、渦層が速度 $\B{v}$ で移動すると仮定する。式(13)の左辺は、渦層の面の単位面積当たりに $(\B{u}_2-\B{u}_1)\B{v}\cdot \B{n}$ を寄与する。右辺第一項は、$(p_2-p_1)\B{n}+(\B{u}_2-\B{u}_1)\B{u}_1\cdot \B{n}$ を寄与する。
検査体積の縁とその体積からの寄与は、層内の力密度に特異性が無い限り無視できる。そのため、これらを当面無視すると、式(13)の成分を $\B{n}$ および $\B{u}_2-\B{u}_1$ とそれぞれ平行な成分が等しいと考えることで、
\begin{split}
p_2 = p_1,\,\, \B{v}\cdot\B{n} = \B{u}_1\cdot \B{n} = \B{u}_2\cdot \B{n} \qquad(14)
\end{split}
が得られる。
これは、オイラー方程式により表現される動力学との一致が、渦層を横切って圧力が連続であり、渦層が流体と共に移動することが要求されることを示している。ゆえに、$S_v(\B{x},t)=0$ が渦層の方程式であるならば、
\begin{split}
\ff{\del S_v}{\del t}+\B{u}_1\cdot \nabla S_v = \ff{\del S_v}{\del t}+\B{u}_2\cdot \nabla S_v=0 \qquad(15)
\end{split}
となることが言える。$\B{u}_1-\B{u}_2$ と $\nabla S_v$ は垂直であることに注意が必要である。
ところで、渦層内の渦線の運動には意味を与えることができる。まずは、渦層上の流体粒子の速度 $\B{q}_v$ を、$\B{q}_v+\nabla\Phi = \B{q}$ で移動する渦層上の点として定義しよう。 ここに $\B{q}_v$ は式(8)で与えられ、$\nabla \Psi$ は外部の非回転速度場、$q=|\B{q}|$ は渦層を挟む両側の平均速度とする。
それでは、渦層内の渦線がこれらの流体粒子と共に移動することを示そう。これは、渦層上の2点 $A$ と $B$ に対して定義される。具体的には、渦層上の積分、循環関数、またはポテンシャルの跳躍を考える。そして、
\begin{split}
\Gamma_{AB} = \int_A^B \big[ \B{u} \big]_1^2\cdot \diff \B{s} \qquad(16)
\end{split}
($\Gamma_{AB}$ は、渦層が縮約不可能な曲線を含む場合は、多値となる可能性がある)今、$\Gamma_{AB}$ は、$A$ と $B$ を結ぶ線を横切る渦層の束度でもあり、これらが同じ渦線上にある場合はゼロとなる。したがって、上式は、以下が示されば従うことが言える。なお、$A$ と $B$ は各点での局所速度 $\B{q}$ で移動するとする。
\begin{split}
\ff{\diff \Gamma_{AB}}{\diff t} = 0 \qquad(17)
\end{split}
我々は、上式に2つの論証を与えることにする。第1の方法は直感的、第2の方法は形式的なものである。これを考えるに当たり、式(17)は速度 $\B{q}$ で移動する点に対しての渦束度の相対的な変化が無いことを述べていることに注意しよう。
さて、渦層が $\eps$ と非常に小さな厚みを持っているとしよう。このとき、図2.2-2に示すように、渦層と共に移動する参照系内で、渦層の断面 $A_1, A_2$ について考える。なお、図2.2-2に示すような固有座標系 $(s,n)$ を用いるとする。ここに、接線方向の速度成分 $u_s$ は以下で近似できる。
$$
u_s =
\left\{
\begin{split}
&\, u_1 \quad \left( n>\ff{1}{2}\eps \right) \EE
&\, u_2 \quad \left( n<-\ff{1}{2}\eps \right) \EE
&\, q+\ff{(u_1-u_2)n}{\eps} \quad \left( -\ff{1}{2}\eps < n<\ff{1}{2}\eps \right)
\end{split}
\right. \qquad(18)
$$
ここに、$\DL{ q=\ff{1}{2}(u_1+u_2) }$ とする。また、渦度(紙面に垂直)は $\om = -\DL{\ff{\del u_s}{\del n}} $ で表され、渦層の強さは $ \DL{ \kappa = \int \om\,\diff n = u_2-u_1} $ となる。そして、$A_1 A_2$ を横切る渦度束は、
\begin{split}
\int \om u_s\,\diff n = -\ff{1}{2}(u_1^2-u_2^2) = \kappa q \qquad(19)
\end{split}
と表せる。これより、速度 $q$ で移動する点に対しての渦度束の相対的な変化は無いことが言える。これが第1の直感的な論証である。
第2の論証は、ケルビンの循環定理を基礎として用いる。渦層上の流体粒子に沿った微分を $\DL{ \ff{\diff}{\diff t} }$ で表し、領域1側の粒子についての微分を $\DL{ \ff{\diff_1}{\diff t} }$ 領域2側の粒子についての微分を $\DL{ \ff{\diff_2}{\diff t} }$ と表すとしよう。すると、我々は次式を得る。
\begin{split}
\ff{\diff}{\diff t} \int_B^A \B{u}_2\cdot \,\diff \B{s} = \int_B^A \left( \ff{\diff_2 \B{u}_2}{\diff t}+(\B{q}-\B{u}_2) \right) \cdot \,\diff \B{s}+\int_B^A \B{u}_2\cdot\,(\diff \B{s}\cdot \nabla \B{q}) \qquad(20)
\end{split}
今、$\DL{ \ff{\diff_2 \B{u}_2}{\diff t}=-\nabla p-\nabla V }$ と置換して、さらに $\B{u}_2 = \B{q}+\ff{1}{2}\big[ \B{u} \big]_2^1 $ と置換する。この置換を適用してある程度の積分を行うと、以下を得る。
\begin{split}
\ff{\diff}{\diff t} \int_B^A \B{u}_2\cdot \,\diff \B{s} &= p_B-p_A+V_B-V_A+\ff{1}{2}q^2\big|_B^A+\ff{1}{8}( \B{u}_1-\B{u}_2 )^2\big|_B^A \EE
&\quad+\int_B^A \ff{1}{2}\Big[ (\B{u}_2-\B{u}_1)\cdot(\diff \B{s}\cdot \nabla)\B{q}-\diff \B{s}\cdot\big( (\B{u}_2-\B{u}_1)\cdot\nabla \big)\B{q} \Big] \qquad(21)
\end{split}
を得られる。1と2を入れ替えても同じ方程式が成立する。式(21)の最後の項の被積分関数を展開すると、
\begin{split}
\ff{1}{2}(\B{u}_2-\B{u}_1)\times \diff \B{s}\cdot\,\text{rot}\,\B{q} \qquad(22)
\end{split}
となることが言える。今、$\DL{ \text{rot}\,\B{q} = \ff{1}{2}( \text{rot}\,\B{u}_1+\text{rot}\,\B{u}_2 )=\B{0} }$ である。このようになるのは、渦層を挟んだ各領域の流れが非回転であるためでる。(実際、式(22)は、外部平均渦度が渦層の接線方向を向いているという条件下で、渦層が回転運動している領域を分離している場合でも消失する。より踏み込んで言えば、(22)が3つの共面ベクトルの3重スカラー積であるためである。)この結果、式(17)は圧力の連続性の観点から直ちに従う。
原理的には、式(8)と(17)は外部速度の値と共に、保存力の存在下での均質流体における渦層の発展を追跡するのに十分な情報を教えてくれる。渦層の強度(式(16)で定義される $\Gamma$ )は、渦層上の原点について、
\begin{split}
\B{\kappa} = \nabla\times \B{n},\quad \nabla\Gamma = \B{n}\times \B{\kappa} \qquad(23)
\end{split}
と表せる。この勾配演算子は渦層内で2次元である。ゆえに、2つの方程式は任意の瞬間にて渦層の位置と強度が与えられたとき、時間毎に渦層の位置と強度を更新するための情報を提供する。ただし、そのような問題が適切に設定されているか、有限時間以上に渡って滑らかな解(無限回の微分が可能な解)を持つかどうかは未解決の問題である。
特に、空気力学的な応用において、定常運動における渦層の形状を研究することは興味深い。定常運動においては、流線と流脈線が一致するため、渦層は両側の流体にとって流れ面であり、また $\B{u}_1$ と $\B{u}_2$ の各々は渦層に平行である。式(17)から、$\B{q}\cdot \nabla \Gamma$ は渦層の流線上で一定であると言え、そのため $\B{q}$ に平行な曲線で一定であることが言える。なお、この定数は必ずしもゼロである必要な無い。式(17)は流線上の2点での $\B{q}\cdot \nabla \Gamma$ の差を表すためである。式(23)を用いると、渦層上で、
\begin{split}
\B{q}\cdot \nabla \Gamma = \B{q}\cdot \B{n}\times \B{\kappa} = -c \qquad(24)
\end{split}
が成立する。ここに $c$ は定数である。今、$\B{q}\times \B{\kappa}$ は $\B{n}$ に平行である。そのため、
\begin{split}
\B{q}\times \B{\kappa} = c \B{n} \qquad(25)
\end{split}
であると言える。$p_1=p_2$ および $V_1=V_2$ であるので、ベルヌーイ定数の差は、
\begin{split}
H_1-H_2 = \ff{1}{2}\big( \B{u}_1^2-\B{u}_2^2 \big) = \B{q}\times \B{\kappa}\cdot\B{n} = c \qquad(26)
\end{split}
となる。外側の流れが非回転であり、$c$ が渦層上で一定である場合、ベルヌーイ定数は層上で一様である。ベルヌーイ定数が同じであれば、$c=0$ であり、渦層上の流線は層の渦線と一致する。すなわち、$\B{q}\times \B{\kappa}$ は平行となる。これは通常の場合である。
上で与えられた結果は、理想的な一様流体が外部流れ場に特異点を持たない場合のものであることを注意して欲しい。密度ないしは保存力が面を横切って不連続である、理想的な一様流体を各々含む2つの領域を分離する物質面は、式(21)から言えるように、渦層となる。 力のポテンシャルが不連続であることも必要であることも注意せよ。この場合、外部の力場の法線成分の不連続は渦層内に渦度を生成しない。(渦を生成するのは、接線成分の跳躍である)
話を法線方向の速度の跳躍に戻そう。このとき、法線方向の速度跳躍は圧力に吸収(転化)される。面内に局在化された特異力(単位面積当たり有限大の力)は、渦層を横切る圧力跳躍を生じさせるが、渦層が流体と共に移動するという結論は変えない。このことは、式(13)から(14)への論証から直ちに得られる。
しかしながら、この状況では式(17)はもはや成立せず、渦層上の線は平均速度 $\B{q}$ とはならない。渦層に平行な面内の特異力は、渦層を流体に対して相対的に移動させる。このような特異力は、例えば渦層が電流がの流れる層である場合は、完全導体流体中に生じるローレンツ力によってや、渦層内に埋め込まれた有限な運動量束を持つ高速ジェットにより生じる可能性がある。後者は、翼のジェットフラップで生じることが示されている。
ところで、2つの非混和流体間の境界では、表面張力が界面を横切る方向には圧力の跳躍が生じ、そのため、この場所では特異な法線力が作用することになる。水波理論やレイリー・テイラー不安定性の理論は、渦層の動力学の特別な場合と見なすことができ、その運動は密度の不連続性により表面に生成された渦層によるものとなる。渦層が流体と共に移動する全ての場合については、渦層の強度の生成は式(20)より従う。ブシネスク?(Bjerknes’s)の理論に基づく代替の定式化もある。
ところで、渦層の最も単純な例は、2つの速度が異なる一様流が、平面の渦層により分離されている場合である。具体的には、$z>0$ の領域では速度が $\DL{\left( -\ff{1}{2}U,0,0 \right)},$ $z<0$ の領域では速度が $\DL{\left( \ff{1}{2}U,0,0 \right)}$ であるとしよう。この状況下では、渦層は $z=0$ の平面となり、その強度は $U\B{j}$ となる。その他の例は、半径 $a$ の断面を持つ円筒形の渦層である。このとき、渦層の渦線は円筒の母線に沿っている。また、速度場は円筒内では $0$、外側では方位角方向で $\DL{ \ff{\kappa a}{r} }$ となる。ここに、$\kappa$ は渦層の強度、$r$ は円筒の軸中心からの距離である。円筒内の一様速度をこの流れに重ね合わせることができて、らせん状の渦線と渦層流線を持つ円筒渦層が得られる。このとき、式(25)が満たされることは容易に確認できる。実用的に重要なのは、翼の後方に形成される渦系である。

コメント