カーデン(Kaden)スパイラルは,相似形をもつ数多くの渦層(ボルテックス・シート)族のうちの一員にすぎない。プラントル(Prandtl, 1922)は,等角(対数)スパイラル形状をもつ二次元・非定常・自己相似の渦層の存在を示した(Küchemann & Weber (1965),Mangler & Weber (1967) も参照)。ここでは、以下の形を仮定しよう。
$$
\begin{split}
Z = t^m f(\q)\, e^{i\q}, \quad \G=t^n g(\q)
\end{split} \qquad(1)
$$
渦層の媒介変数方程式 $f$ と $g$ は実数である。Birkhoff–Rott 方程式(1.6)に代入すると、この形の解を得るには$n=2m-1$( $t$ のべき乗が打ち消されるため)が必要であり、このとき $f$ と $g$ は以下の複素微積分方程式を満たすことが分かる。
$$
\begin{split}
e^{-i\q}\left\{ mf+(1-2m)\ff{g}{g’}(f’-if) \right\} = -\ff{i}{2\pi}\, \RM{p.v.}\int \ff{ \hat{g}’ \diff \hat{\q} }{ fe^{i\q}-\hat{f}e^{i\hat{\q}} }
\end{split} \qquad(2)
$$
ここに、プライム「$’$」は $\theta$ による微分,ハット「^」は $\theta=\hat{\q}$ での評価を表す。この複素微積分方程式は、$f$ と $g$ に関する 2 つの実方程式とできて、ここに以下の実関数の形を試そう。
$$
\left\{
\begin{split}
&\, f=Ae^{\A\q} \EE
&\, g=Be^{\beta\q}
\end{split} \quad (-\infty<\q<\infty) \qquad(3)
\right.
$$
そして、代入と整理により、次の式が得られる。
$$
\begin{split}
e^{(2\A-\beta)\q}A^2\big\{ m+\beta(1-2m)(\A-i) \big\} = -\ff{iB\beta}{2\pi}\, \RM{p.v.}\int_{-\infty}^{\infty} \ff{ e^{\beta\phi} }{ 1-e^{(i+\A)\phi} }
\end{split} \qquad(4)
$$
この方程式は $\beta = 2\A$ のときしか満たされない。しかし (4) の積分は $\A$ と $\beta$ の符号が同じ、かつ $|\beta|<|\A|$ でないと発散する。発散の原因は無限遠での渦度の非有界性(渦層強度は $\kappa \propto e^{(\beta-\A)\theta}$ のように比例して成長)にある。ただし $0<\beta<\A$ の範囲では、
$$
\begin{split}
\RM{p.v.} \int_{-\infty}^{\infty} \ff{e^{\beta \phi} \diff \phi}{ 1-e^{(i+\A)\phi} } = \ff{\pi i}{i+\A}\left\{ \ff{1+e^{u}}{1-e^{u}} \right\}, \quad u=\ff{2\pi i\beta}{i+\A}
\end{split} \qquad(5)
$$
このような評価により,$\beta=2\A$ の場合には解析接続で積分を定義できる。すると
$$
\begin{split}
\ff{A^2}{B\A}\left\{ m(\A+i)+\ff{1}{2\A}(\A^2+1)(1-2m) \right\} = \ff{1+e^u}{1-e^u}
\end{split} \qquad(6)
$$
実部と虚部から $A^2/B$ を消去すると、
$$
\begin{split}
\ff{1}{m} = \ff{2}{1+\A^2}-\ff{2\A}{1+\A^2}\cdot \ff{ \sinh \ff{4\pi \A}{1+\A^2} }{\sin \ff{4\pi \A^2}{1+\A^2} }
\end{split} \qquad(7)
$$
が導かれ、$-\infty < m < 1/2$ が従う。
このとき解の形は、$r = A t^{m} e^{\alpha\theta}, \quad \Gamma = B t^{2m-1} e^{2\alpha\theta}$ ここに、$A^2/B = \RM{fn}(\A),$ $r^2=(A^2/B)\G t$ で、渦度は外向きに移動する。また、$\DL{\frac{\diff\theta}{\diff t}_{\G} = -\frac{2m-1}{2\A t}}$ より、角速度は $r$ の増加とともに遅くなることが分かる。
つまり、時間経過と共に渦の任意の素片は伸長し、直線化され、減速していくことが言える。例えば、半径 $r$ の円内の循環 $\G$ は $1/t$ のように減少する。なお、時間 $t$ は正負のいずれでもよい。もし $t<0$(解が時間逆行)なら,ある時刻で全域で発散する流れが生じうる。
ところで、今考えている複素ポテンシャル $w(z)$ は以下のように与えられる。
$$
\begin{split}
\ff{\diff w}{\diff z} = u-iv = -\ff{i}{2\pi} \ff{B}{A} t^{m-1} \int_{-\infty}^{\infty} \ff{e^{\beta \hat{\q}} }{ \ff{z}{At^m}-e^{i(\A+i)\hat{\q}} }\diff \hat{\q} \propto t^{m-1} \left( \ff{z}{t^m} \right)^{ \ff{\A-i}{\A+i} }
\end{split} \qquad(8)
$$
そのため、
$$
\begin{split}
w \propto t^{2m-1} \left( \ff{z}{t^m} \right)^{ \ff{2\A}{\A+i} }
\end{split} \qquad(9)
$$
であると言える。
前述の式変形は、D. W. Moore (1972) の未発表の論文に基づいている。彼は、解析接続を用いて無限遠における渦度から発散寄与を差し引くという手法を導入した。この発散は、$\B{\om}$ が無限遠で十分速くに消滅しない場合、§1.1 のポアソン型積分によって与えられる $\B{u}$ の $\B{\om}$ の積分表現が、$\rot{\B{u}}=\B{\om}$ の解の有効な表現ではないという事実から生じる。
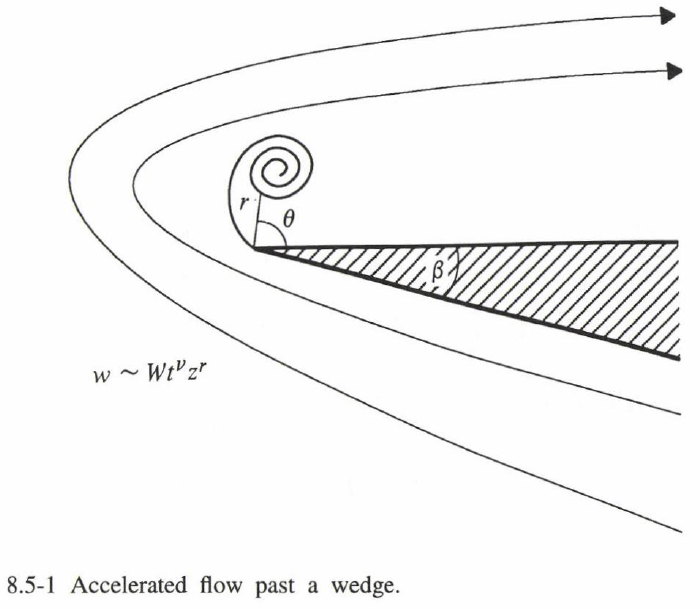
例えば、$r→\infty$ のときに $\om=\om(r)→\infty$ となるような 2 次元流れの単純なケースを考えることにしよう。速度は明確に定義されているが、積分表現は発散する。この場合、解析接続が適切となる。Alexander [1971]は、プラントル解を $N$ 枚の多分岐構造に一般化し、以下の式を示している。
$$
\begin{split}
Z_p = t^m f(\q)\, \exp\left( \ff{i\{\q+2\pi(p-1) \} }{N} \right) \quad(1\leq p \leq N)
\end{split} \qquad(10)
$$
論理展開はここまでと同じように進むが、唯一の変更点は (7)式における $m$ と $α$の関係である。最後の項の引数において、$4π$ は $4π/N$ に置き換えられる。
式(1)で表されるタイプの相似解(ただし $m>1/2$ であるためプラントル等角螺旋のクラスには属さない)は、カーデン問題の一般化(Pullin [1978]、Pullin and Phillips [1981])($m=2/3$ の場合)で生じる。図8.5-1(Blendermann [1969])に示すように、角度 $β$ のくさびを通過する加速流れを考えと、渦放出がない場合、複素ポテンシャルは、以下の様になる。
$$
\begin{split}
w = -Wt^{\nu} z^{\mu}
\end{split} \qquad(11)
$$
ここに $\nu$ は与えられた正の数であり、$W$ は $L^{2-μ}T^{-1-\nu}$ の次元を持つ正の次元定数である。指数 $μ$ については $β$ と次の関係にある。
$$
\begin{split}
\mu = \ff{\pi}{2\pi-\beta}
\end{split} \qquad(12)
$$
このとき,くさびの面上では $\Im w=0$ となる。もし $\beta<\pi$ なら先端の速度は無限大となる。ここで、クッタ条件を用いて先端から渦層が剥離することを許すことにする。すると、複素ポテンシャルは、渦層とそのくさび形における像による追加の項 $w_v$ を持ち、次元解析から、以下の形であることが言える。
$$
\begin{split}
w_v = W^{\ff{2}{2-\mu}} t^{ \ff{2\nu+\mu}{2-\mu} } f\left( \ff{z}{W^{\ff{1}{2-\mu}}\,t^{\ff{1+\nu}{2-\mu}} }\right)
\end{split} \qquad(13)
$$
これは、$w$ と $\G$ が同じ次元を持つため、(1) と同じ形の解が得られ、
$$
\left\{
\begin{split}
&\, m = \ff{1+\nu}{2-\mu} \EE
&\, n = \ff{2\nu+\nu}{2-\mu}
\end{split} \qquad(14)
\right.
$$
であることが分かる。
$2m -1=n$ であることに注意しよう。このような条件では、くさび内の像渦度、適切な端条件、そしてくさび先端におけるクッタ条件を含めて (2) を解くという問題に帰着することになる。この条件は、先端に近づく流線が滑らかに分離すると仮定する形で与えられる。$β >0$ の場合は、くさびの風下側先端によどみ点があることを意味する。流れは非定常であるため、これは分離渦層を横切る圧力の連続性には反しない。
$0<\beta <\pi,\, \DL{ \ff{1}{2}< \mu < 1 }$ そして、ゆえに $\DL{ m>\ff{1}{2} }$ なら $\nu > 0$ となる。厳密解について現状、分かっていないが,スパイラル中心近傍はカーデン・スパイラル(Kaden spiral)と同様に解析できる。スパイラル中心の位置はこのように与えられる。
$$
\begin{split}
Z_T = W^{\ff{1}{2-\mu} } t^m\, \zeta_0
\end{split} \qquad(15)
$$
ここに、$\zeta_0$ は全体解により決まる定数で、スパイラル中心近傍の局所解析だけでは定まらない。さて、ここに局所極座標 $r,\theta$ を $Z_T$ 中心にとり,半径 $r$ で測った循環を $\G$ としよう。このとき次元解析より、
$$
\begin{split}
\G = k^{1/m}\, r^{2-\ff{1}{m}}, \quad \big(k\propto W^{\ff{1}{2-\mu}} \big)
\end{split} \qquad(16)
$$
であると言える。
さらに、$\DL{ r\ff{\diff \q}{\diff t} = \ff{\G}{2\pi r} }$ であることから、$\q = \ff{\G t}{2\pi r^2}$ であることが言えて、それゆえ、
$$
\begin{split}
r = k\left( \ff{t}{2\pi \q} \right)^m
\end{split} \qquad(17)
$$
が中心近傍でのスパイラルについての方程式であることが言える。これに対応する、パラメトリック表示はこのようになる。
$$
\begin{split}
Z = W^{\ff{1}{2-\mu} } t^m\, \zeta_0+\left( \ff{\G^m}{k} \right)^{\ff{1}{2m-1}} \exp \left( \ff{ itk^{ \ff{2}{2m-1} } }{\G^{\ff{1}{2m-1} } } \right)
\end{split} \qquad(18)
$$
別解として、式(2)を用いても、積分の分母を考察できる。積分範囲は、螺旋の中心の $θ=\infty$ から、くさびの先端と交わるある値 $θ_0$ まで範囲となる。計算は、次のように近似できる。まず、$θ$ が増加すると $f(θ)$ が減少することに注目しよう。$\hat{θ}<θ$ の場合 $fe^{i\q}-\hat{f}e^{i \hat{\q}} ≈ -\hat{f}e^{i \hat{\q}} $ となって、積分はゼロを中心に振動する。一方、$\hat{θ}>θ$の場合、積分の分母は $fe^{iθ}$ を中心に振動する。そこで、積分を次のように置き換えることができる。
$$
\begin{split}
\ff{1}{fe^{i\q}} \int_{\q}^{\infty} \hat{g}’ \diff \hat{\q} = -\ff{g(\q)}{ f(\q)e^{i\q} }
\end{split} \qquad(19)
$$
(なお、基本的には、$\DL{ \int_0^{2\pi} \ff{\diff \q}{1-\eps e^{i\q}} =0\,\,(\eps>1) },$ ないしは $\eps>1$ で $2\pi$ という結果を用いている。)今、(2) を2つの実方程式に分離して、
$$
\left\{
\begin{split}
&\, mf+(1-2m)g\,\ff{f’}{g’} = 0 \EE
&\, 2\pi(1-2m)f^2 = g’
\end{split} \qquad(20)
\right.
$$
これの解は、
$$
\left\{
\begin{split}
&\, g = c\,\q^{1-2m} \EE
&\, f = \left( \ff{c}{2\pi} \right)^{1/2} \q^{-m}
\end{split} \qquad(21)
\right.
$$
特に興味深い特殊なケースがいくつかある。例えば $β =0, μ=1/2, ν=0, m=2/3$ の場合、半無限平板の衝撃運動となる。Anton [1939])。Rott [1956] は、くさび形に衝突する弱い衝撃波によって引き起こされる運動を考察している。今、$u_0$ を衝撃波を横切る速度変化の振幅、$a_0$ を音速とすると、流れは非圧縮性流れに等価となり、以下の速度ポテンシャル $w$($u_0$ に関して線形)を課せられる。
$$
\begin{split}
w = Ku_0\,a_0\,t\left( \ff{z}{a_ot} \right)^{\mu}
\end{split} \qquad(22)
$$
ここで、$K$ はくさびによる音響パルスの回折の解によって与えられる無次元定数である。一般形(13)と比較すると、$\nu=1-μ$ であり、したがって $m=1$ であることがわかる。また、$W=Ku0\,a0^{1-\mu}$ である。すると、螺旋の中心の位置 $Z_T$ は、スケーリングに従って以下のように振舞う。
$$
\begin{split}
\ff{Z_T}{a_0 t} \propto \ff{W^{\ff{1}{2-\mu}} }{a_0} = K^{\ff{1}{2-\mu}} M^{\ff{1}{2-\mu}}
\end{split} \qquad(23)
$$
ここに、$M=u_0/a_0$ は、流れのマッハ数とする。
相似法は、円錐対称性を持つ定常三次元流れに適用できる。この場合、すべての流量は $x/\tilde{z}$ と $y/\tilde{z}$ の関数となる( $z$ は対称軸)。例えば、速度ポテンシャルは $\phi=\tilde{z}\,\RM{fn}(x/\tilde{z},y/\tilde{z})$ で表され、螺旋は $r=\sqrt{x^2+y^2}=\tilde{z}\,f(θ)$ で表される。細長体理論は、例えば速度 $U$ の細長いデルタ翼を流れる流れに適用でき、この場合 $\tilde{z}↔Ut$ という同値関係が成り立つので、$m = 1$ の相似解のクラスに属することになる。
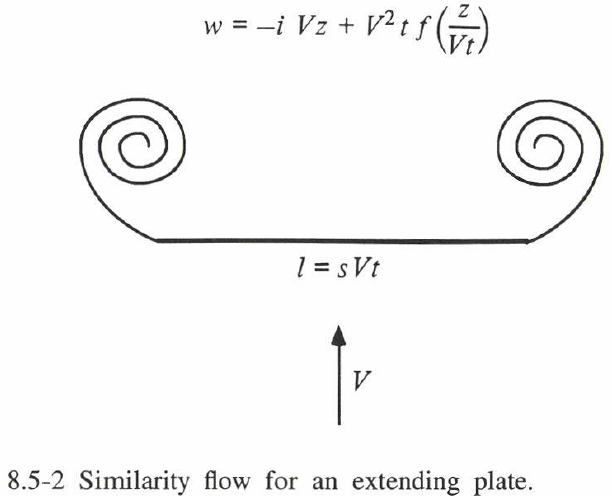
細長いデルタ翼を過ぎる流れの場合、等価な 2 次元問題(Smith [1968]、図8.5-2参照)は、長さが $sVt$ のように膨張する平板に垂直な速度 $V$ を持つ自己相似流れに帰着できる。自己相似速度ポテンシャル $w$ は、($m=1,n=1$ に対応して)以下の形をとる。
$$
\begin{split}
w = -iVz+V^2t\cdot f\left( \ff{z}{Vt} \right)
\end{split} \qquad(24)
$$
二枝スパイラル ($N=2$) (式(10)参照)は,無限渦層の巻き上がりや,Moore 特異性(§8.3)発生後の初期段階を表すのに都合がよい。たとえば,強度 $\kappa = U$ の一様渦層とすれば、この渦層は $\pm \DL{\ff{1}{2}}U$ と流れを分離なら、原理的には $r = \pm Ut\,f(\q)$ の二枝スパイラルへ巻き上がる可能性がある。このとき、Birkhoff-Rot 方程式 のパラメータ表示は、
$$
\begin{split}
Z = \pm Ut\, \zeta\left( \ff{\G}{U^2 t} \right) \quad\,\, (0<\G<\infty)
\end{split} \qquad(25)
$$
ここに、$\zeta(\tau) \sim \tau$ つまり、$\tau \to \infty$ であり、そして以下のようになることが言える。
$$
\begin{split}
\zeta(\tau) \sim \ff{\tau}{\lambda} \exp \left( \ff{i\lambda^2}{\pi \tau}+i\eps \right) \quad\,\, (\tau \to 0)
\end{split} \qquad(26)
$$
さて、$\lambda = 1$ として Betz 近似を用いるとしよう。ただし、このような解が存在するかは未証明であり、よしんば、解が存在しないことを示唆する数値計算の結果(Pullin, 1989)すら存在する。
より一般的な場合として、次のような初期分布が二枝スパイラルに巻き上がる場合を考えよう。(ただし $q>0$)
$$
\begin{split}
Z = \pm A\,\G^q \quad\,\, (0\leq \G<\leq \infty)
\end{split} \qquad(27)
$$
このときのスパイラルのパラメータ表示はこのようになる。
$$
\begin{split}
Z = \pm \ff{t^m}{A^n}\, \zeta(\tau) \quad\,\, \left( \tau = \ff{\G A^2 n}{t^n} \right)
\end{split} \qquad(28)
$$
ここに、$\DL{ n=\ff{1}{2q-1} }$ かつ $m = nq$ とする。
関数 $\zeta (\tau)$ は、Birkhoff-Rot 方程式 の特異積分微分方程式を満たし,境界条件 $\zeta(\infty) \sim \tau^q,\,\, |\zeta(\tau)|\sim \DL{ \ff{\tau^q}{\lambda},\,\,(\tau \to 0) }$ を備える。
ここに $\lambda$(圧縮/引き締め係数)は未定定数であり、全体の解から定まるものである。スパイラルが膨張するには $m>0$ が必要で,したがって $q$ は $\DL{\ff{1}{2} < q < \infty,\,\, \infty >m>\ff{1}{2} }$ の範囲となる。特に $q=1$ で初期の渦層強度 $\kappa\propto X^{\ff{1}{q}-1}$ は $x=0$ で有限($q<1$)か、無限大($q>1$)かの質的変化が生じる。
よって、$r \to 0,\, \G\to0,\, \tau\to0$ の極限での螺旋の漸近形状は、このようになる。
$$
\begin{split}
r = \ff{A \G^q}{\lambda}
\end{split} \qquad(29)
$$
$\q$ に対する依存性は以下から導けて、
$$
\begin{split}
2\pi r v_{\q} = 2\pi r^2 \dot{\q} = N\G \quad (N=2)
\end{split} \qquad(30)
$$
それゆえ、このようになる。
$$
\begin{split}
\q = \ff{t \G}{\pi r^2}+\eps = \ff{\lambda^2}{\pi \tau^{1/n}} + \eps
\end{split} \qquad(31)
$$
したがって、
$$
\begin{split}
\zeta(\tau) \sim \ff{\tau^q}{\lambda} \exp \left( \ff{i\lambda^2}{\pi \tau^{1/n}}+i\eps \right) \qquad( \tau\to 0)
\end{split} \qquad(32)
$$
これに、Betz の仮説を適用すると、やはり $\lambda = 1$ となる。
ところで、$q \geq 1$ かつ $m \leq 1$ ならば、スパイラルの全長は無限大となる。さらに、(29) と (31) から $\G$ を消去するとこのようになる。($\G$ を消去すると孤長積分が発散する)
$$
\left\{
\begin{split}
&\, r \sim \left( \ff{t}{\q \pi} \right)^m \left( \ff{\lambda}{A} \right)^n \EE
&\, s \sim \int^{\infty} r\,\diff \q
\end{split} \qquad(33)
\right.
$$
今、$r=0$ における渦度は以下のように必ず特異であり、式 (30) よりこのようになる。
$$
\begin{split}
\om = \ff{N}{2\pi r} \ff{\diff \G}{\diff r} \sim \ff{1}{\pi q}\left( \ff{\lambda}{A} \right)^{\ff{1}{q}} \ff{1}{r^{1/m}}
\end{split} \qquad(34)
$$
ただし、これは積分可能な特異点である。
Pullin (1989) は、$q$ の範囲を変えて Birkhoff-Rot 方程式 に似た方程式の数値解を調べている。$\DL{ \ff{1}{2}<q<1 }$ の範囲については、彼は非スパイラル解や単枝スパイラルの分離解を得ている。このとき、スパイラルは有限長で、$q$ が $1$ よりわずかに大きい範囲でも単枝・二枝スパイラルが見いだされる。
単枝は二枝と異なり $\lambda>1$ をとり,Betz の議論から単枝の $\lambda$ については $\DL{ \lambda = \ff{1+q}{q} }$ が与えられる。もっとも,これらの相似解をMoore 特異性プロファイルに接続して,スパイラル形成後の渦層進化を完全に描くことはまだ達成されていないことに留意する必要がある。

コメント