単一値ポテンシャルを持つ保存力によって作用する完全正圧流体において、第一のヘルムホルツ法則(§1.5)は流体粒子に渦度を与えることは不可能であると述べ、ケルビンの循環定理(§1.6)は物質回路周りの循環が初期にゼロであればゼロのままであることを示している。
さて、粘性、非保存力、または傾圧効果に訴えることなく渦度が創造可能かという疑問が生じる。これらが初期に存在すれば、後続運動において重要でない理由はア・プリオリには存在しないため、これらの効果に訴えることなく渦度が創造可能かを知りたいというのが本節の主題である。
Klein [1910] はこの問題を彼の Kaffeelöffel 実験で扱った(Betz [1950]も参照)。結論として、ヘルムホルツおよびケルビン定理は区分的連続渦度の生成を排除するが、渦シートの形成や循環の生成は阻止しないということであった。
Klein の実験について考えよう。幅 $2a$ の二次元平板が、平板に垂直な速度 $U$ で完全非圧縮流体中を運動するとする。複素ポテンシャル $w(z) = \phi + i\psi, z = x + iy$ を導入する。境界条件は $\psi = Uy\,\,\text{on}\,\,x = 0, |y| < a$(軸は瞬間的に平板と一致し、$y$ 軸は平板に沿い、$x$ 軸は運動方向にとる)、および $w \sim 0$ as $z \to \infty$(無限遠での循環は許されない)である。標準的方法(例えば Batchelor [1967 §6.5])または直接計算により、
$$
\begin{split}
w = U(z-\sqrt{a^2+z^2})
\end{split} \qquad(1)
$$
が得られる。平板上では、
$$
\begin{split}
\phi = \mp U\sqrt{a^2-y^2},\quad x = \pm0
\end{split} \qquad(2)
$$
$$
\begin{split}
v = \ff{\del \phi}{\del y} = \pm\ff{Uy}{\sqrt{a^2-y^2}}, \quad x = \pm 0
\end{split} \qquad(3)
$$
さらに、仮想運動量は $x$ 方向を向いており、その大きさは
$$
\begin{split}
I_B = \oint \phi\,\B{n}\cdot \B{i}\,\diff s = 4U \int_0^a \sqrt{a^2-y^2}\,\diff y = \pi U a^2
\end{split} \qquad(4)
$$
その運動エネルギーは、
$$
\begin{split}
\iint \ff{1}{2}(\nabla \phi)^2\,\diff x\diff y = \ff{1}{2}\oint \phi\,\ff{\del \phi}{\del n} \diff s = -2\int_0^a \phi\, \ff{\del \phi}{\del x} \,\diff y = \ff{1}{2}\pi U^2 a^2
\end{split} \qquad(5)
$$
さて、$A$ から $A’$ への瞬間的な流線周りの循環は、例えば、
$$
\begin{split}
\int_A^{A’} \B{u}\cdot \diff \B{s} = \phi(A’)-\phi(A) = 2U\sqrt{a^2-y^2}
\end{split} \qquad(6)
$$
である。したがって平板での強さは、
$$
\begin{split}
\kappa = \ff{2U y}{\sqrt{a^2-y^2} }
\end{split} \qquad(7)
$$
の渦シートと等価である。束縛渦度 $\om(x,y)$ は以下で表される。
$$
\begin{split}
\om = \ff{2Uy\,\delta(x) }{\sqrt{a^2-y^2} } \qquad (y<a)
\end{split} \qquad(8)
$$
束縛渦度の流体力学的インパルス $\B{I}_V$ は、
$$
\begin{split}
\B{I}_V = \int \B{r}\times \B{k}\,\om\, \diff x\diff y = \B{i}\oint \kappa y\,\diff y = \B{i}\int_0^a \ff{4 Uy^2}{\sqrt{a^2-y^2} } \diff y = \pi U a^2\B{i}
\end{split} \qquad(9)
$$
となる。ここに、$\B{I}_B = \B{I}_V$ に注意せよ。なぜなら、物体の体積は $0$ であるためである。束縛渦度の運動エネルギーは、
$$
\begin{split}
\ff{1}{2}\int \om \phi\,\diff x\diff y = \ff{1}{2}\int_a^{-a} Uy\kappa\,\diff y = \ff{1}{2}\pi U^2a^2
\end{split} \qquad(10)
$$
束縛渦度の運動エネルギーと物体周りの流れの運動エネルギーの差は、物体内部の流体流れの運動エネルギーであるが、この場合、速度が有界で体積がゼロであるため、これもゼロとなる。したがって(5)と(10)で与えられる値は同じである。(静止流体中を速度Uで運動する物体によって引き起こされる非回転流の運動エネルギーの一般表現は $\DL{ \ff{1}{2}\B{I}_B\cdot \B{U} }$ である。)
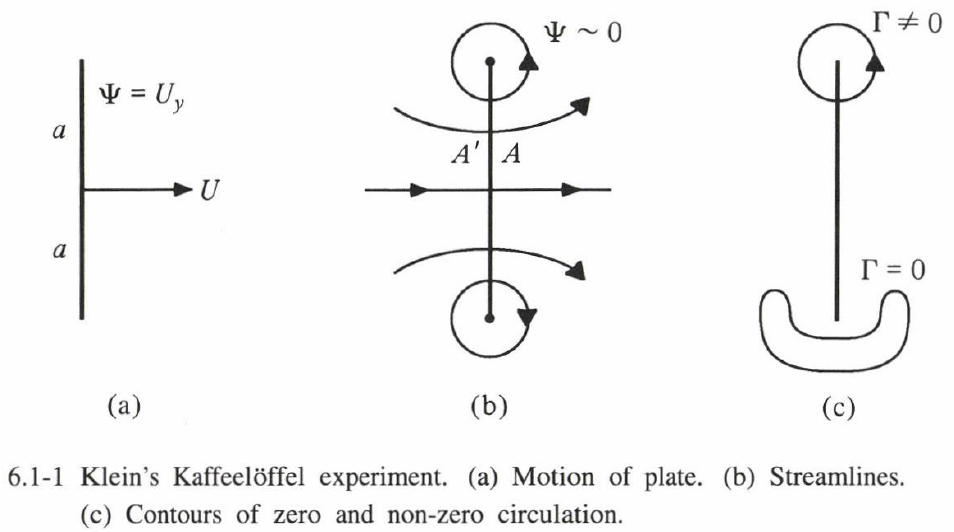
Kleinは、平板が除去される(コーヒースプーンを抜き取る)か溶解される(確実に「思考」実験では可能)と、渦層が流体中に残ると論じた。図6.1-1に示すように描かれた回路周りに非ゼロ循環が創造された。流体粒子は渦度を獲得せず、流体内に完全に存在する閉じた輪郭周りに循環が生成されていないため、ヘルムホルツ-ケルビン法則との矛盾はない。循環を持つ新しい輪郭は事前には閉じておらず、それらは物体と交差していた。これは流れのトポロジー的性質を変えることによって、シート(つまり特異分布)として渦度が創造された例である。

コメント