カルマン渦列とは、流れに直交する物体の後流において自然に形成される二重列の反対回転渦構造である。それぞれの渦は、反対符号の循環を持つペアとして配置され、上下2列に交互に並ぶ。この配置は、von Kármán(1911)によって、流れの安定条件から理論的に導かれた。
レイノルズ数が約 100 の範囲で存在する鈍頭物体の背後に見られる、交互に並んだ二重渦列はよく知られた観察結果である。Lamb [1932 $370a] は、Ahlborn [1902]、Benard [1908]、Karman and Rubach [1913] の記述を参照している。
Lugt [1979 p.7] は、9世紀のアッシリアの格子模様を紹介している。この格子模様は、レオナルド・ダ・ヴィンチのスケッチにもはっきりと描かれていることを付記しておく。
理想的な状態として、点 $z_m=ma$ における強度 $-\gamma$ の逆回転する点渦と、点 $\DL{z=\left( m+\ff{1}{2} \right)a+ih,\, -\infty< m < \infty }$ における強度 $γ$ の点渦の無生物的な二重列である。このときの複素ポテンシャルは、
$$
\begin{split}
w = \ff{i\gamma}{2\pi} \log \left( \sin \ff{\pi z}{a} \right)-\ff{i\gamma}{2\pi} \log \left\{ \sin \ff{\pi}{a} \left( z-\ff{1}{2}a-ih \right) \right\}
\end{split} \qquad(1)
$$
$y→\pm ∞$ のとき $w→0$ となることに注意。さらに、$z=0$ における渦の速度は、
$$
\begin{split}
W = -\ff{i\gamma}{2a} \cot \left( -\ff{\pi}{2}-\ff{i\pi h}{a} \right) = \ff{\gamma}{2a}\tanh \ff{\pi h}{a}
\end{split} \qquad(2)
$$
対称性から、各渦は無限遠点における流れに対して同じ速度 $W$ で運動する。微小擾乱に対する安定性は Karman によって議論されている。ここでは Lamb[1932 § 156] の手法に従うこととする。下段の渦は $x$ 方向と $y$ 方向にそれぞれ $\big(\A(t), \beta(t) \big)e^{2\pi imp} $ だけ変位し、上段の渦は $\big(\A'(t), \beta'(t) \big)e^{2\pi imp} $ だけ変位する。今、一般性を失うことなく、$0≦p≦1$ とできて、さらに $p$ は無次元分数調波数と見なすことができる。
§5と同様の解析により、$k=h/a$ を経路のアスペクト比として定義する以下の方程式が得られる。
$$
\left\{
\begin{split}
&\,\ff{2\pi a^2}{\gamma}\ff{\diff \A}{\diff t} = -A\beta-B\A’-C\beta’ \qquad(3) \EE
&\,\ff{2\pi a^2}{\gamma}\ff{\diff \beta}{\diff t} = -A\A-C\A’+B\beta’ \qquad(4) \EE
&\,\ff{2\pi a^2}{\gamma}\ff{\diff \A’}{\diff t} = A\beta’-B\A+C\beta \quad\qquad(5) \EE
&\,\ff{2\pi a^2}{\gamma}\ff{\diff \beta’}{\diff t} = A\A’+C\A+B\beta \quad\qquad(6) \EE
\end{split}
\right.
$$
ここに、
$$
\left\{
\begin{split}
&\, A = \pi^2\big\{ 2p(1-p)-\RM{sech}^2 k\pi \big\} \qquad(7) \EE
&\, B = i\pi^2 \left\{ 2p\ff{ \cosh k\pi(1-2p) }{\cosh k\pi}+\ff{\sinh 2k\pi p}{\cosh^2 k\pi} \right\} \qquad(8) \EE
&\, C = \pi^2 \left\{ \ff{ \cosh 2\pi kp }{\cosh^2 k\pi}-2p \ff{\cosh k\pi(1-2p)}{\cosh k\pi} \right\} \qquad(9) \EE
\end{split}
\right.
$$
であるとする。
各 $p$ に対して、2つの擾乱モードが考えられる。$\A=\A’, \beta=-\beta’$ の対称モードと、$\A=-\A’, \beta=\beta’$ の反対称モードとなる。
どちらのモードであっても、同じ安定性特性を持ち、その解は $e^{\sigma t}$ に比例する。ここに、
$$
\begin{split}
\sigma = \mp B+(A^2-C^2)^{1/2}
\end{split} \qquad(10)
$$
とすると、対称モードの場合は $ -B$、非対称モードの場合は $+B$ となる。$A$ と $C$ は実数であるため、安定であるには $A^2 ≦ C^2$ が必要となる。
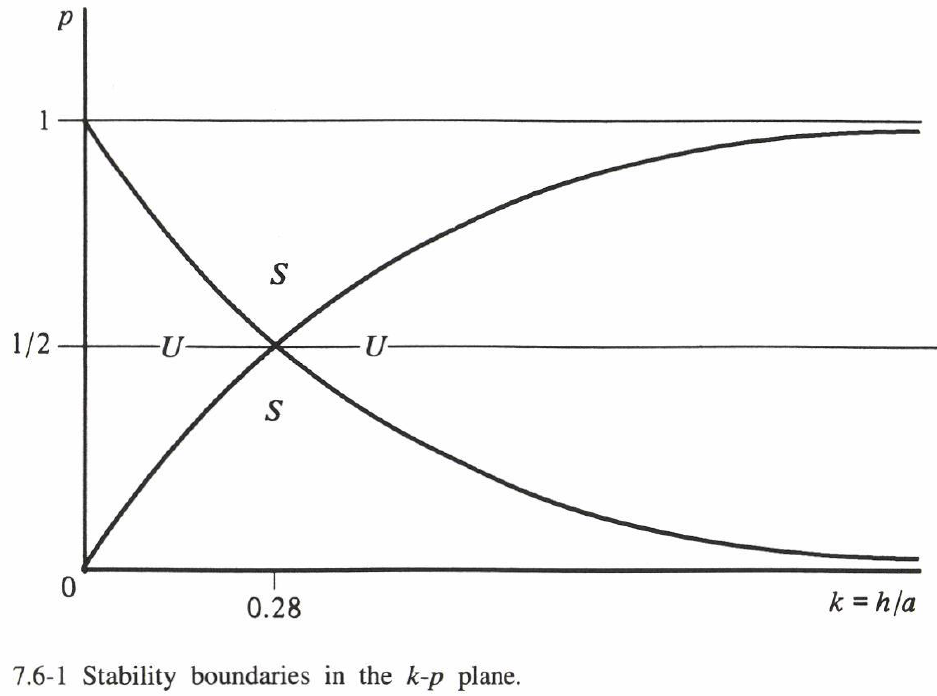
図7.6-1に、$k-p$ 平面に曲線 $A^2=C^2$ をプロットしている。$p=1/2$ に関する対称性は、$\DL{x→x+\ff{1}{2}a}$ の並進に対する不変性から生じる。 図から明らかなように、$k$ の各値に対して、曲線が交差する特別な値 $k_c$ を除いて、擾乱が不安定となる波数の範囲がある。なお $k≠k_c$ の場合にて、常に波数が不安定になるわけではなく、不安定化に必要なのは1つの波数だけとなる。$k_c$ の臨界値は、(7)と(9)に $p=1/2$ を代入することで得られ、以下のようになる。
$$
\begin{split}
k_c = \ff{1}{\pi}\sinh^{-1} 1 = 0.2801\cdots
\end{split} \qquad(11)
$$
この特定の $k_c$ 値では、経路はあらゆる微小外乱に対して安定であるが、有限振幅外乱に対して安定であるとは限らない。Kochin, Кlibel, および Roze [1964] は、リアプノフ法を適用して、有限振幅の不安定外乱が存在することを実証している。
Domm [1956] は、簡潔なデモンストレーションを行ている。$p=1/2$ での渦対の不安定モードを考えてみよう。擾乱の基本セルは、上列に 2 つ、下列に 2 つ、合計 4 つの渦で構成されている。そして、この配列は 4 つの列に分割され、各列は $2a$ で区切られた渦で構成され、(1) のような複素ポテンシャルを生じる。
したがって、8 つの座標は、8 つの一次非線形常微分方程式からなる系を満たす。4 つの渦の、平衡位置に対する複素変位を、系と共に移動する参照系、つまり無限遠の流れに対する相対速度を $W$ として、同様に $\zeta_1,\zeta_2, \zeta_3, \zeta_4$ とする。ここで、$\zeta_1$ と $\zeta_2$ は上段、$\zeta_3$ と $\zeta_4$ は下段とする。正確な方程式は積分を持つ。
$$
\begin{split}
\zeta_1+\zeta_2-\zeta_3-\zeta_4 = K
\end{split} \qquad(12)
$$
これはインパルスの不変性の結果である。さらに、以下の様に書くと、
$$
\left\{
\begin{split}
&\, \Phi = \zeta_1-\zeta_2+\zeta_3-\zeta_4 \EE
&\, \Psi = \zeta_1-\zeta_2-\zeta_3+\zeta_4
\end{split} \qquad(13)
\right.
$$
Domm は、2階の項を保持したまま、このように書けることを示し、
$$
\left\{
\begin{split}
&\, \ff{\diff \Phi}{\diff t} = \ff{\gamma \pi}{4a^2}\left(1+\ff{\pi K}{2a} \right)\Psi \EE
&\, \ff{\diff \Psi}{\diff t} = -\ff{\gamma \pi}{4a^2}\left(1-\ff{\pi K}{2a} \right)\Phi
\end{split} \qquad(14)
\right.
$$
$\sinh k\pi=1$ のとき、$Φ$ と $Ψ$ は $e^{\sigma t}$ に比例する。ここで、
$$
\begin{split}
\sigma^2 = -\ff{\gamma^2 \pi^2}{64a^4} \left(1-\ff{\pi^2}{4a^2}K\bar{K}+\ff{\pi}{2a}(K-\bar{K}) \right)
\end{split} \qquad(15)
$$
を導入しよう。
そして、初期変位が $\Im K\neq 0$(つまり、列が横方向に均等に変位していない)となる場合、擾乱は指数関数的に増大するが、その速度は擾乱の振幅に比例する。したがって、カルマン渦列はすべてのアスペクト比 $k$ に対して不安定となるが、$k = k_c$ の場合には、増大速度は擾乱の振幅に依存する。
Karman [1911, 1912] および Karman and Rubach [1913] は、鈍い物体の背後の不安定な後流をモデル化し、運動量の考察から、物体の抗力と流れの特性との関係を導き出した。物体を固定した基準系において、物体の下流のある地点における後流を、回転しない流体によって分離された強度 $\pm \Gamma$ の渦度領域に分離することが可能であると仮定する。これらの領域は、物体に対して横方向距離 $h$ 離れており、速度 $U_0-U_s$ で下流に移動するとする。ここに、$U_0$ は自由流の速度である。流れは周期 $\tau$ で周期的になり、ここに
$$
\begin{split}
\tau = \ff{a}{U_0-U_s}
\end{split} \qquad(16)
$$
という関係である。

そして $a$ は渦の下流方向の分離定数である。ここで、図7.6-2に示すように、物体に対して固定された領域 $\mathscr{A}$ における運動量バランスを考える。この領域の下流境界 $\sum(t)$ は時間とともに周期的に移動する。$\B{I}$ を領域(物体を含む)の流体力学的インパルスとすると(物体は束縛渦度分布と外力密度 $-\B{F}$ に置き換えられる)、物体にかかる抗力 $\B{D}=(D, L)$ は、
$$
\begin{split}
\B{D} = \int_{\mathscr{A}} \B{F}\, \diff A
\end{split} \qquad(17)
$$
と表される。(§3.10参照)このとき、
$$
\begin{split}
\ff{\diff \B{I}}{\diff t} = -\B{D}+\int_{\mathscr{A}} \B{u}\times \B{\om}\,\diff A+\int_{\sum} (\B{u}\cdot \B{n}) (\B{\om}\times \B{r}) \diff s-\int_{\sum} (\B{q}\cdot \B{n})(\B{\om}\times \B{r})\diff s
\end{split} \qquad(18)
$$
ここに、$\B{q}$ は $\sum(t)$ における速度とする。第一の積分については以下のように表せる。
$$
\begin{split}
\oint_{\del \mathscr{A}} \left\{ \ff{1}{2}\B{u}^2 \B{n}-\B{u}(\B{u}\cdot \B{n}) \right\}\diff s
\end{split} \qquad(19)
$$
最後の 2 つの項は、$\sum$ が完全に非回転流体中にある場合、ゼロとなる。ここで、(18) 式の周期 $\tau$ にわたっての時間平均をとり、自由流に対する相対速度を $\B{u’}=\B{u}-\B{U}_0$ と書くとする。今、$\DL{ \overline{ \int_{\mathscr{A}}\B{\om}\,\diff A } }$ なので、(19) 式の $\B{u}$ を $\B{u’}$に置き換えることができる。
さらに、(19) の中身は、等高線が非回転流体中にある間は、等高線の存在に依存しない。ここに、$\B{q}$ を、$\sum(t)$ が非回転流体中にあるようなものと仮定する。ただし、$\B{q}$ が瞬間的に(無限速度で)ジャンプし、$\mathscr{A}$ から 2 つの渦が通過して物体における新しい渦の発生を相殺する場合を除く。この場合以下が成立する。((18) の 2 番目の積分からの寄与は、被積分関数が無限小時間のみ非ゼロであるため、ゼロとなる)
$$
\begin{split}
\tau \overline{\B{D}} = \tau \int_{\sum} \left\{ \ff{1}{2}\B{u’}^2 \B{n}-\B{u’}(\B{u’}\cdot \B{n}) \right\}\diff s+\int \diff t\int_{\sum} (\B{q}\cdot \B{n})(\B{r}\times \B{\om})\diff s
\end{split} \qquad(20)
$$
最後の項は $γh \B{i}$ で、$h$ は渦の重心の垂直方向の変位である。最初の項は $\DL{ -\ff{1}{2}\int \big\{ (u^2-v^2)\diff y-2uv\,\diff x \big\} }$ となる。したがって、
$$
\begin{split}
\overline{D} = \ff{\gamma h}{a}(U_0-U_x)-\ff{1}{2}\Im \int_{-i\infty}^{i\infty} \overline{ \left( \ff{\diff w}{\diff z} \right)^2 }\, \diff z
\end{split} \qquad(21)
$$
ここに、$w$ は、渦無し流れにおける複素ポテンシャルとする。
点渦列のカルマン渦列によって与えられる $w(z)$ の特別な場合では、最後の項は評価(Goldstein [1965 §243])により、以下のように与えられる。
$$
\begin{split}
\ff{\gamma^2}{2a^2}\left( \ff{a}{\pi}-h\tanh \ff{\pi h}{a} \right)
\end{split} \qquad(22)
$$
そして、このとき、$U_s = W$ を代入すると、以下が成立して、
$$
\begin{split}
\overline{D} = \ff{\gamma^2}{2a\pi}+\ff{\gamma h}{a}
\end{split} \qquad(23)
$$
SaffmanとSchatzman [1982b]は、有限コア皮質の渦列後流の非粘性モデルを研究し、コアサイズが抗力、アスペクト比、渦強度の関係に及ぼす影響を調査している。

コメント