二次元領域において、有限の面積を持つ回転が一様な連結領域であり、かつ周囲が非回転(渦無し)の流体に囲まれているものを渦班 (vortex patch) と呼ぶ。
渦班の境界は渦跳躍(§2.1)である。渦層・渦班(渦層によって囲まれた渦班)も大いに興味深い。空洞な渦層・渦班(密度ゼロの流体が渦シートで囲まれている)や、停滞渦層・渦班(非回転流体が渦シートで囲まれている)では、渦班内部の渦度はゼロとなる。非ゼロの渦度を含む渦層・渦班は Prandtl–Batchelor 流とも呼ばれ、鈍頭物体まわりの完全流(非粘性流)のモデルとしても重要である。
非一様渦班(すなわち、複数の領域から成り、それぞれが一様だが異なる渦度をもっている)は、連続的に変化する渦度場をモデル化できる。Moore [1978] は、有限だが小さい厚みをもつ渦層によって形成される渦班を研究している。彼は、小さな厚みの効果が Birkhoff–Rott 方程式に項を付加することで記述できることを示し、その結果、次式が得られることを示している。
$$
\begin{split}
\ff{\del \overline{Z}}{\del t} = -\ff{i}{2\pi}\, \RM{p.v.} \int \ff{\diff \G’}{ Z(\G)-Z(\G’)}-\ff{i}{6\om}\ff{\del}{\del \G} \left( \ff{ \del \overline{Z}/\del \G }{ | \del Z/\del \G |^4 } \right)+O(\eps^2)
\end{split} \qquad(1)
$$
ここに、$Z(\G, t)$ は渦の中心線のパラメーター表示であり、$\om$ は定数渦度である。式の展開は、$\eps = \overline{h}/\rho$ の冪により計算される。( $\overline{h}$ は渦層の厚み、$\rho$ は曲率半径を表し、$\overline{\kappa} = \om \overline{h}$ は一定値を保つ) そのため補正項のオーダーは、$\DL{ \ff{\overline{\kappa} \overline{h} }{\rho} }$ である。 $\om$ は力学的に定まる定数であり、$\overline{h}$ は定義によって定数であるが、厚み $h$ と局所渦層強度 $\kappa = \om h$ は一般には変化する。
Moore は、形式的な整合漸近表現法(ヒューリスティックな方法)によって(1)を導出した。ここでは、経験的な議論によってこの方程式を再導出する。まずは、有限厚さの影響は、2つの異なる作用に分解できることに注目する。第1には、渦層の曲率によって渦層に沿った渦度流束が変化し、循環とともに移動するラグランジュ点の速度が変化する。第2に、渦層に沿った渦層の厚さの変化によって、渦層方向に直交する渦層の運動が変化する。今、中心線に沿った弧の長さを $s$、中心線の接線と $x$ 軸の間の角度を $\q$ とする。このとき、以下が成立する。
$$
\left\{
\begin{split}
&\, \ff{\del Z}{\del \G} = \ff{e^{i\q}}{\kappa} \EE
&\, \diff Z = e^{i\q}\diff s \EE
&\, \ff{\del \G}{\del s} = \kappa \EE
&\, \ff{\del \q}{\del s} = \ff{1}{\rho} \EE
&\, \ff{\del \kappa}{\del s} = \om\ff{\del h}{\del s}
\end{split} \qquad(2)
\right.
$$
また、Moore の補正項 $\DL{ \ff{\del \overline{Z}}{\del t} }$ は次のように書ける。
$$
\begin{split}
-\ff{\kappa^2}{6\rho\om}e^{-i\q}-\ff{i}{2\om}\,\kappa \ff{\del \kappa}{\del s}e^{-i\q}
\end{split} \qquad(3)
$$
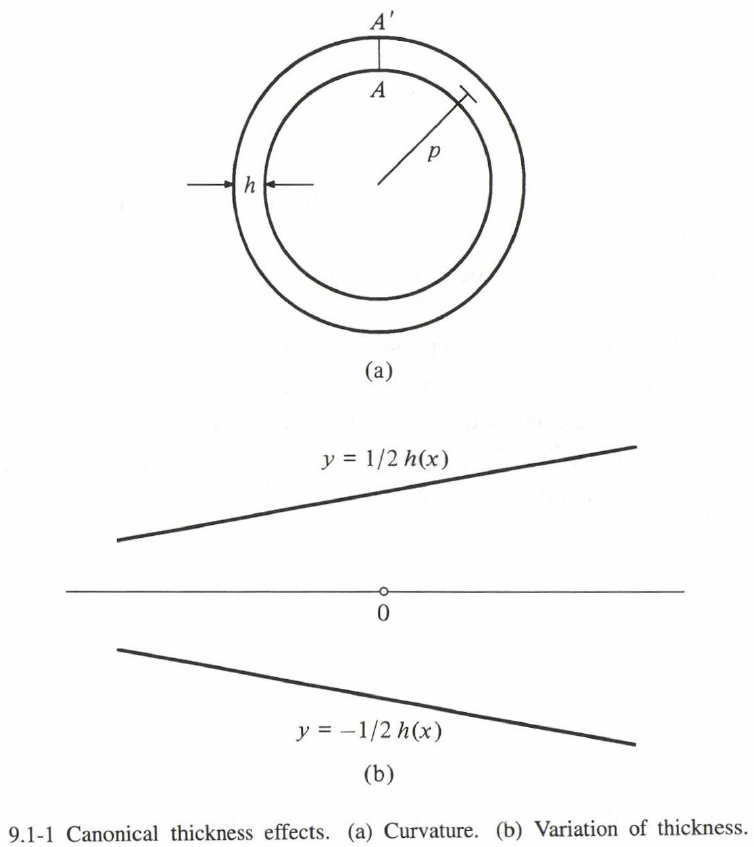
第1項は渦層の接線方向(曲率効果は $\rho \to \infty$ で消滅)であり、第2項は法線方向(この効果は $\partial h/\partial s = 0$ で消滅)である。曲率効果を計算するには、円形渦層を考えれば十分である(図 9.1-1a)。渦層内の接線速度 $v(r)$ は、$\om = \DL{ \ff{1}{r}\ff{\diff (rv)}{\diff r} },$ $v(\rho-h/2) = 0$ より、
$$
\begin{split}
v = \ff{1}{2}\om \left(r-\ff{ \left( \rho-\ff{1}{2}h \right)^2 }{r} \right) ,\quad\,\, \left( \rho-\ff{1}{2}h<r<\rho+\ff{1}{2}h \right)
\end{split} \qquad(4)
$$
といえる。
また、渦度流束から定義される速度はこのようになる。
$$
\begin{split}
\ff{1}{\om h} \int_{\rho-\ff{1}{2}h}^{\rho+\ff{1}{2}h} \om v\, \diff r = \ff{\kappa}{2}-\ff{\kappa h}{6\rho}+O\left( \ff{h^2}{\rho^2} \right)
\end{split} \qquad(5)
$$
(5) による追加速度は、ちょうど (3) の第一項に一致する。
(渦層の)厚みが法線速度に与える影響を計算するには、中心線上の点 $O$ における誘導法線速度 $V$ の差 $\hat{V}$ を考えれば良い。図 9.1-1b に示すように、厚み $h(x)$ が変化する渦層と、厚みがゼロで強度が同じ渦層の場合の差 $\hat{V}$ は以下の様に与えられる。
$$
\begin{split}
\hat{V} &= \RM{p.v.}\int_{-\infty}^{\infty} \diff x \left\{ \left[ \int_{-\ff{1}{2}h(x)}^{\ff{1}{2}h(x)} \ff{-x}{x^2+y^2}\ff{\om\,\diff y}{2\pi} \right]+\ff{\om h}{2\pi x} \right\} \EE
&= \ff{\om}{2\pi}\,\RM{p.v.}\int_{-\infty}^{\infty} \left\{ \ff{h}{x}-2\tan^{-1} \ff{h}{2x} \right\}\diff x
\end{split} \qquad(6)
$$
これを $y$ について積分すると次のようになる。すなわち、$y$ についての部分積分を行うと以下を得る。
$$
\begin{split}
\hat{V} &= \ff{\om}{2\pi}\,\RM{p.v.}\int_{-\infty}^{\infty} \ff{h^2}{4} \left( \ff{h}{x}-h’ \right) \ff{\diff x}{x^2+h^2/4}
\end{split} \qquad(7)
$$
$h\to 0$ の極限での値を得るため、$h = h_0+\eps x$ を考え、$\eps \to 0$ とすることを考える。いくつかの解析の結果、以下が得られる。
$$
\begin{split}
\RM{p.v.}\int_{-\infty}^{\infty} \ff{h^2}{4} \left( \ff{h}{x}-h’ \right) \ff{\diff x}{x^2+h^2/4} \sim \pi h_0 \eps = \pi h\ff{\diff h}{\diff x}
\end{split} \qquad(8)
$$
それゆえ、
$$
\begin{split}
\RM{p.v.}\int_{-\infty}^{\infty} \ff{h^2}{4} \left( \ff{h}{x}-h’ \right) \ff{\diff x}{x^2+h^2/4} \sim \pi h_0 \eps = \pi h\ff{\diff h}{\diff x}
\end{split} \qquad(9)
$$
が見いだされる。これは、Moore の公式(式(3))の第2項と一致する。
Moore は、この修正方程式が運動量・角運動量・エネルギーについて $O(\eps)$ のオーダーの精度で保存することを示し、また、これを厚みが $h$ の渦層のケルビン–ヘルムホルツ不安定(§8.2)に適用し、擾乱による渦層の挙動を解析した結果、以下の式を見出している。なお、$a(t), b(t)$ は時間についての複素関数とする。
$$
\begin{split}
Z = \ff{\G}{U}+a(t)\exp \left( \ff{ik\G}{U} \right)+b(t)\exp\left( -\ff{ik\G}{U} \right)
\end{split} \qquad(10)
$$
さらに、$a,b$ を線形化して、Moore は以下を得た。
$$
\begin{split}
\ff{\diff \overline{a}}{\diff t} = \ff{iUkb}{2}-ik^2Uh(2b+\overline{a})
\end{split} \qquad(11)
$$
そして、$a$ と $b$ を入れ替えた同じ式を検討する。すると、これらの式から、擾乱が $e^{σt}$ のように増大することを示唆している。ここで $\sigma$ はこのようになる。
$$
\begin{split}
\sigma = \ff{1}{2}Uk \left[ \left(1-\ff{kh}{3} \right) (1-kh ) \right]^{\ff{1}{2}}
\end{split} \qquad(12)
$$
(12)に至る近似は、$tan≪ 1$ の場合にのみ有効であり、このとき、
$$
\begin{split}
\sigma ≈ \pm \ff{1}{2} Uk\left[ 1-\ff{2}{3}kh \right]
\end{split} \qquad(13)
$$
となる。
これは、Rayleigh [1880,1945 §367] による、有限厚さの渦層の微小安定性に関する解析と一致する。また、幅 $h$ の層上の微小擾乱に対する正確な分散関係は、
$$
\begin{split}
\sigma^2 = \ff{U^2}{H^2} \big[ e^{-2kh}-(1-kh)^2 \big]
\end{split} \qquad(14)
$$
のようになる。
これから、$kh=1.28$ のとき不安定性は消失するはずである。Moore の近似は $kh=1$ のとき安定化を示すが、$kh>3$ のとき疑似不安定性を示す。Moore の修正 Birkhoff–Rott 方程式(1.6)の適切性は未解決の問題であるが、$kh$ が大きいときに Birkhoff–Rott 方程式の場合よりも大きな割合で不安定性が生じる。それゆえ、修正方程式は原方程式より特異的であることが示される。

コメント