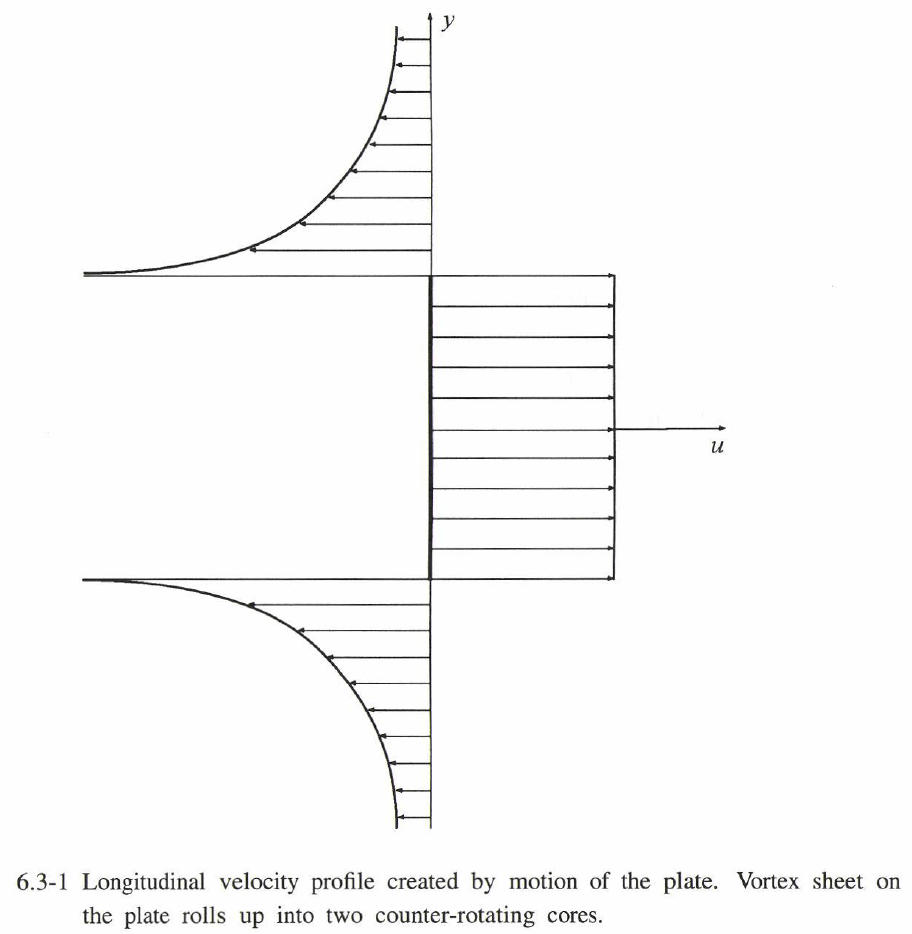
平板の除去により創造された渦層は平衡解とはならない。$x = 0$ での縦方向速度プロファイルを図6.3-1に示す。束縛渦度に対する力の特異性は、誘導速度場の特異性によって現れる。渦層のその後の発展は大変興味深い問題である。適切な方程式は§8.1で得られ、解の構造は§8.4で記述される。ここでは定性的議論に限定することにする。
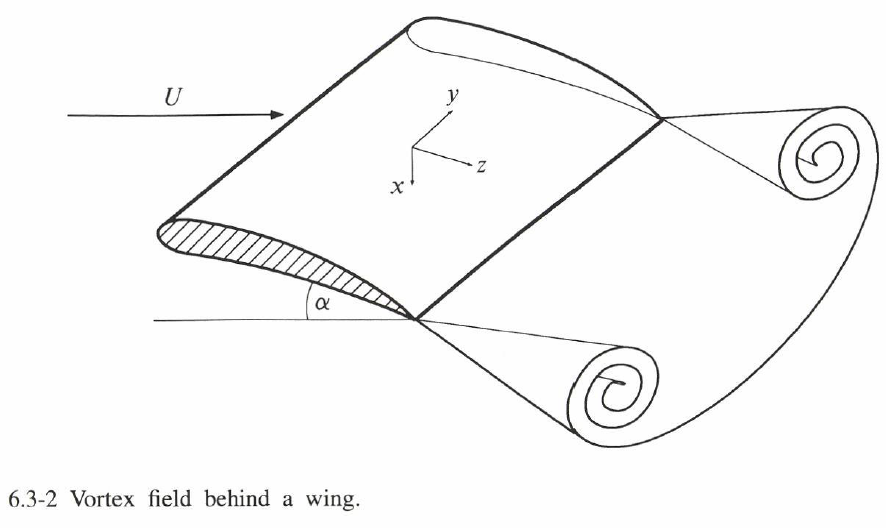
この問題は、航空機の後流との関連で重要である。第1近似としては、矩形で楕円荷重を持つスパン $2a$ の翼の下流距離 $Z$ での流れは、小迎え角 $\A$ での速度 $W$ の流れ中で、$U = W\A$(図6.3-2参照)と識別して、平板が除去された後の時刻 $t = Z/W$ での発達する渦層のそれである。
渦層は、渦度が最大となる翼の先端(先端では計算上、速度が無限大となる)によって引き出され、渦巻きに巻き込まれながら成長し続ける螺旋に引き込まれ、渦層をさらに巻き込んでいく。粘性がない場合、渦層は無限に薄いままであるが、巻き上がりは続き、連続する巻きの間の距離もゼロとなり、渦層が連続的に引き伸ばされてその強度(すなわち速度の跳躍)がゼロに減少する螺旋を与える。螺旋はほぼ円対称である。速度場の漸近性は確定的ではないが、おそらく連続で至る所微分不可能な分布に近づく。
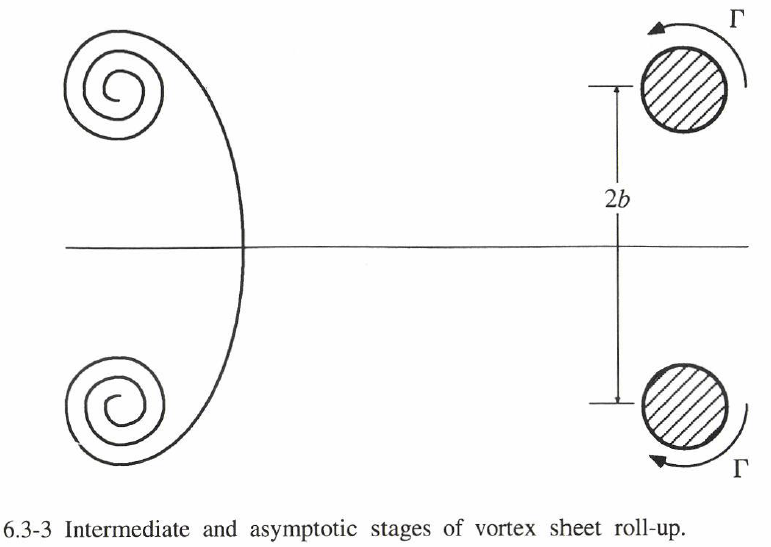
この場合、粗視化近似の性質を推定できる。渦層の巻き上がりの計算に基づき、渦像の巻き上がりの粗視化限界は、中心が距離 $b$ 離れた強度 $\pm \Gamma$ の二つのほぼ円形の反回転渦であると仮定する(図6.3-3参照)。巻き上がりは流体力学的インパルスを保存する(これは粘性存在下でも真である(§3.6))。さらに循環が保存される(すなわち、中心線 $y = 0$ を横切る渦度拡散がない)と仮定される。すると、
$$
\begin{split}
\Gamma = \int_0^a \kappa\,\diff y = 2Ua
\end{split} \qquad(1)
$$
上式のように渦強度を与える。分離距離 $b$ は、元の渦層と渦対の流体力学的インパルスの $x$ 成分を等しく置くことから求められる。
$$
\begin{split}
\int_{-a}^a y\,\kappa(y)\,\diff y = \pi Ua^2 = \Gamma b
\end{split} \qquad(2)
$$
これより、
$$
\begin{split}
b = \ff{1}{2}\pi a
\end{split} \qquad(3)
$$
であることが言える。
もう一つ、コアのサイズおよび内部の渦度分布を推定することが残っている。(歴史的理由で)ここではエネルギー保存に基づくPrandtl [1919]の議論を与えるが、現在では、角インパルス保存に基づくBetz [1932]の議論によって取って代わられている(§8.4参照)。これらの議論は、渦層が漸近的に一対の線渦に巻き上がるという、素朴な信念と矛盾する結論を導く。さて、Prandtlは渦度がコア内で一定で、半径 $\delta$ を持ち、コア変形は無視できると仮定した。すると、
$$
\begin{split}
\pi \delta^2 \om = \Gamma = 2Ua
\end{split} \qquad(4)
$$
この近似に対して、コア内の速度は大きさ $\DL{ \ff{\Gamma r}{2\pi \delta^2} }$ の接線方向を向く。したがって、コア内流体の運動エネルギーは、以下のように計算できる。
$$
\begin{split}
E = \int_0^{\delta} 2\pi r\left( \ff{\Gamma r}{2\pi \delta^2} \right)^2\diff r = \ff{\Gamma^2}{8\pi}
\end{split} \qquad(5)
$$
コア外部の運動については、以下で与えられる流れ関数 $\psi$ を持つ。
$$
\begin{split}
\psi = -\ff{\Gamma}{2\pi} \log \left( \ff{r}{r’} \right)
\end{split} \qquad(6)
$$
ここに、$r$ と $r’$ はコア中心までの距離である。そのため、コア外部での流体の運動エネルギーは、
$$
\begin{split}
-\ff{1}{2}\oint_{\text{cores}} \psi\,\ff{\del \psi}{\del n}\,\diff s
\end{split} \qquad(7)
$$
第1のコアでは、
$$
\begin{split}
\psi ≈ \ff{\Gamma}{2\pi}\log \left( \ff{b}{\delta} \right) + O\left( \ff{\delta}{b} \right), \qquad -\oint \ff{\del \psi}{\del n}\,\diff s = \Gamma
\end{split} \qquad(8)
$$
したがってコア外部流体の運動エネルギーは、近似的に、$\DL{ \ff{\Gamma^2}{2\pi}\log \left( \ff{b}{\delta} \right) }$ である。初期の渦層の運動エネルギーは(1.5)で与えられる。Prandtl に従って巻き上がり中に運動エネルギーが保存されると仮定すると(Durand [1934 vol. II p. 328]も参照)、
$$
\begin{split}
\ff{\Gamma^2}{8\pi}+\ff{\Gamma^2}{2\pi} \log \left( \ff{b}{\delta} \right) = \ff{1}{2}\pi U^2a^2 = \ff{\pi \Gamma^2}{8}
\end{split} \qquad(9)
$$
これより、
$$
\begin{split}
b ≈ 0.11 b
\end{split} \qquad(10)
$$
が導かれる。
コア半径が接線速度が最大となる距離として定義される場合(§2.1参照)、推定値(10)は通常測定される値よりもやや大きく、Prandtl のモデルは不適切と思われる。(もちろん、仮定された渦度分布の運動エネルギーをより正確に計算することは可能である。
SpreiterとSachs [1951]は剛体円筒に囲まれた一様渦の運動エネルギーを正確に計算している。しかし、渦の表面は渦層となり、この計算の妥当性は明確でない。)コア内の一様渦度の仮定が不一致の原因と思われる(§8.4参照)。

コメント