単一の線状渦が平面壁の近くに存在する場合、その問題は鏡像法(method of images)によって容易に解くことができる。例えば、壁に対して法線方向の速度がゼロになるという運動学的境界条件を満たすなら、反対符号の強さを持つ鏡像渦を壁の反対側に置けば良い。すると、この渦対は壁に平行な方向に速度、$\DL{ U = \ff{\kappa}{4\pi h} }$ で移動することになる。ただし、$\kappa$ は渦の強さ、$h$ は渦から壁までの距離である。
さて、壁に対して平行な強さ $\ff{\kappa}{4\pi h}$ の一様流を渦に重ね合わせると、渦を静止状態に留めることもできる。
より複雑な問題は、平行な2つの壁の間に存在する反対回転渦対(counter-rotating vortex pair in a parallel-sided channel)である。この場合、鏡像系は無限に続く二重の列(doubly infinite row)となり、解析には複素変数法を用いるのが便利である(Batchelor [1967, §6.5] 参照)。まず、以下のような複素ポテンシャル $w(z)$ を導入することにしよう。
$$
\left\{
\begin{split}
&\,w(z) = \phi+i\psi \EE
&\,z = x+iy
\end{split}
\right. \qquad(1)
$$
ここに、$w$ は $z$ の解析関数であり、速度成分 $(u,v)$ は次式で与えられる。
$$
\begin{split}
\ff{\diff w}{\diff z} = u-iv
\end{split} \qquad(2)
$$
単一の強さが線状渦 $\kappa$ が位置 $z_0$ にある場合、複素ポテンシャルは次のように与えられる。
$$
\begin{split}
w = -\ff{i\kappa}{2\pi}\log(z-z_0)
\end{split} \qquad(3)
$$
次に、平行壁チャネル内における反対回転渦対を考える。チャネルの幅を $b$、2つの渦の距離を $b – 2h$ とし、原点を下側の壁上に取り、$x$ 軸を壁に平行な方向とする。このとき、複素ポテンシャルは次式で与えられる。
$$
\begin{split}
w = \ff{i\kappa}{2\pi}\log \ff{z-i(b-h)}{z-ih}+W(z)
\end{split} \qquad(4)
$$
ここに、$W$ はチャネル内において解析関数であり、$x\to \pm \infty$ にて消失し、$\mathscr{F}(w)=0$ となるのは壁面上となる。 $W$ を求める際は、チャネルを上半平面に等角写像する操作をすれば良い。具体的にはこのような操作である。
$$
\begin{split}
\zeta = e^{\ff{\pi z}{b}}, \quad z = \ff{b}{\pi}\log \zeta
\end{split} \qquad(5)
$$
これにより、渦は点 $e^{ \ff{i\pi h}{b} }$ と点 $-e^{ -\ff{i\pi h}{b} }$ に写像される。$\zeta$ 平面では、複素共役点における像を用いて、
$$
\begin{split}
w = -\ff{i\kappa}{2\pi}\log \ff{\zeta-e^{ \ff{i\pi h}{b} }}{\zeta-e^{ -\ff{i\pi h}{b} }}+\ff{i\kappa}{2\pi} \log \ff{\zeta+e^{ -\ff{i\pi h}{b} }}{\zeta+e^{ \ff{i\pi h}{b} }}
\end{split} \qquad(6)
$$
渦が壁に近い場合、鏡像法で求めたポテンシャル(式4)は、次のように解釈できる。この流れ場においては、$z = i h$ に位置する渦の速度成分 $(U, V)$ は、もう一方の渦および鏡像系からの寄与の和として与えられる。鏡像系を上半平面に写像するため、次のような共形写像を用いる。
$$
\begin{split}
U-iV &= \ff{\diff}{\diff z} \left[ \ff{i\kappa}{2\pi} \log\big( z-i(b-h) \big)+W(z) \right]_{z=ih} \EE
&= \lim_{z\to ih}\ff{\diff}{\diff z}\left\{ w+\ff{i\kappa}{2\pi} \log(z-ih) \right\}
\end{split} \qquad(7)
$$
ここに、$w$ は(6)で与えられる $\zeta$ の関数で、$\DL{ w+\ff{i\kappa}{2\pi} \log(\zeta-e^{\ff{i\pi h}{b} } }$ が解析関数であり、我々は以下を得る。
$$
\begin{split}
U-iV &= \ff{ \ff{\diff}{\diff \zeta}\left( w+\ff{i\kappa}{2\pi}\log \big(\zeta-e^{\ff{i\pi h}{b}} \big) \right) }{ \ff{\diff}{\diff z}+\ff{i\kappa}{2\pi}\ff{\diff}{\diff z}\log\left( \ff{z-ih}{\zeta-e^{\ff{i\pi h}{b} } } \right) }
\end{split} \qquad(8)
$$
これの右辺を、$\zeta = e^{\ff{i\pi h}{b} }$ として評価すると、
$$
\begin{split}
\ff{z-ih}{\zeta-e^{\ff{i\pi h}{b}}} = \ff{\diff z}{\diff \zeta}+\ff{1}{2}\ff{\diff^2 z}{\diff \zeta^2}\big( \zeta-e^{\ff{i\pi h}{b} } \big)
\end{split}
$$
となって、$\zeta = e^{\ff{i\pi h}{b} }$ として微分を評価すると、(8)の最終項は、
$$
\begin{split}
\left. \ff{i\kappa}{4\pi} \ff{ \ff{\diff^2 z}{\diff \zeta^2} }{\left( \ff{\diff z}{\diff \zeta} \right)^2} \right|_{\zeta = e^{\ff{i\pi h}{b} }}
\end{split} \qquad(9)
$$
代入と評価により、
$$
\begin{split}
U = \ff{\kappa}{2b \tan\left( \ff{2\pi h}{b} \right) }, \quad V=0
\end{split} \qquad(10)
$$
$h→0$ および $h→b/2$ のときに正しい極限が得られることは容易に検証できる。渦は $h=b/4$ のとき定常となる。そして、複素ポテンシャル(6)は次のように表される。
$$
\begin{split}
w = \ff{i \kappa}{2 \pi} \log \ff{ \sinh \ff{\pi}{b}(z-ih) }{ \sinh\ff{\pi}{b}\big(z-i(b-h)\big) }
\end{split} \qquad(11)
$$
次に興味深い例として、円柱後流におけるフィップル渦対(Föppl vortex pair)を考えることにする。
円柱の半径を $a$、一様流を $U$ とする。2つの渦がそれぞれ $z_0, \bar{z}_0$ にあり、強さがそれぞれ $-\kappa,$ $\kappa$ であるとする。このとき、鏡像渦は $a^2/\bar{z}_0, a^2/z_0$ に生じ、それぞれの強さは $\kappa, -\kappa$ である。したがって、複素ポテンシャルは次式で表される。
$$
\begin{split}
w = U\left(z+\ff{a^2}{z} \right)+\ff{i\kappa}{2\pi}\log \left( \ff{z-z_0}{z-\bar{z}_0} \ff{z-a^2/z_0}{z-a^2/\bar{z}_0} \right)
\end{split} \qquad(12)
$$
これは適切な特異点と無限遠での挙動を持ち、$r=a$ において $\mathscr{F}w = 0$であることが容易に証明される。渦は、以下の条件を満たすとき静止している。
$$
\begin{split}
\ff{\diff }{\diff z} \big[ w-i\kappa\log(z-z_0) \big]_{z=z_0} = 0
\end{split} \qquad(13)
$$
3つの実数未知数 $κ,x_0,y_0$ に対して2つの方程式が存在する。簡約後、式(2.4.7)と式(2.4.8)が満たされる場合、式(13)が満たされることがわかる。
フィップル(Föppl)はまた、円柱の代わりに平板(plate)を用いた場合(流れに垂直な平板)も検討している(Villat [1930], Smith and Clark [1975] 参照)。その結果、平板の端でのKutta条件(端点で速度が有限である条件)を満たすような渦の位置と強さを見つけることは不可能であることが示している。
すなわち、流れの速度は平板端で発散する。Roy [1972] は、渦に吸い込み(sink)を重ね合わせることでKutta条件を満たすことができると示し、この流れは安定であると主張している。
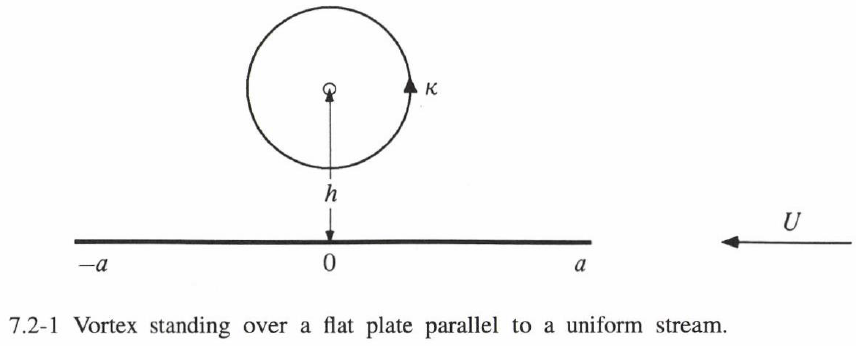
次に、非対称配置の流れを考える。これは、物体と渦の配置が対称でない場合である。たとえば、長さ $2a$ の平板の中央上方に、強さ $\kappa$ の渦を距離 $h$ だけ離して置く場合を考える。なお、平板は速度 $U$ の一様流中に置かれ、流れ方向は負の $x$ 方向とする(図7.2-1参照)。この場合の共形写像は次式で与えられる。
$$
\begin{split}
\zeta = z+\sqrt{z^2-a^2}, \quad z=\ff{1}{2}\left( \zeta+\ff{1}{\zeta} \right)
\end{split} \qquad(14)
$$
これにより、平板は円に写像され、渦の位置は $\zeta = ih+i\sqrt{a^2+h^2}$ に移される。このとき、複素ポテンシャルは次の形になる。
$$
\begin{split}
w = -\ff{U}{2}\left(\zeta+\ff{a^2}{\zeta} \right)-\ff{i\kappa}{2\pi}\log (\zeta-ih’)+\ff{i\kappa}{2\pi}\log \left(\zeta-\ff{ia^2}{h’} \right)-\ff{i\gamma}{2\pi}\log \zeta
\end{split} \qquad(15)
$$
ここに、$h’=h+\sqrt{a^2+h^2}$ と $\gamma$(実数)は任意で、円の中心における境界線渦の強さである。平板周りの循環は、
$$
\begin{split}
\Gamma = \gamma-\kappa
\end{split} \qquad(16)
$$
となる。
この流れでは、渦が定常となり、板の両端でクッタ条件が満たされるように $h, \kappa, \gamma$ を選択することが可能となる。$z=\pm a$ において写像は特異であるため、クッタ条件は、
$$
\begin{split}
\ff{\diff w}{\diff \zeta} = 0 \quad\,\, \text{on}\,\,\, \zeta = \pm a
\end{split} \qquad(17)
$$
これは、以下の評価を導く。
$$
\begin{split}
\ff{\gamma}{\kappa} = \ff{h’^2-a^2}{h’^2+a^2}
\end{split} \qquad(18)
$$
このとき、自由流中の渦が静止するためには、
$$
\begin{split}
\ff{\diff}{\diff \zeta} \left( w+\ff{i\kappa}{2\pi}\log \big(\zeta-ih’ \big) \right)+ \ff{i\kappa}{4\pi} \ff{ \ff{\diff^2 z}{\diff \zeta^2} }{ \left( \ff{\diff z}{\diff \zeta} \right)^2 } = 0
\end{split} \qquad(19)
$$
$\zeta = ih’$ のとき、以下が得られる。( $a\leq h’ \leq \infty$ )
$$
\begin{split}
\gamma = \ff{\pi U(h’^2-a^2)^2(h’^2+a^2) }{2a^2 h’^3}
\end{split} \qquad(20)
$$
平板上の揚力 $L$ は、自由流中の渦に働く渦力と等価であり、その束縛渦度は以下のように計算される。
$$
\begin{split}
L = U(\kappa+\gamma-\kappa) = U\gamma
\end{split} \qquad(21)
$$
ただし、流れの安定性は、不安定なクッタ条件を伴うため、難しい問題であることを付け加えておく。

コメント