線渦の特異分布を $\B{\om}$ に代入すると、インパルスの表現は有限となる。曲線 $\B{R}(s)$ 上にある強さ $\Gamma$ の線渦は、以下のインパルスを持つ。
$$
\begin{split}
\B{I} = \ff{1}{2}\oint \B{R}\times \diff \B{s} \qquad(1)
\end{split}
$$
そして、角運動量インパルスは、
$$
\begin{split}
\B{A} = -\ff{1}{2}\oint \B{R}^2\diff \B{s} \qquad(2)
\end{split}
$$
渦の外側の流体は、多価速度ポテンシャル $\phi$ を持つ非回転運動である。また、$\phi$ は線渦が貫く閉回路周りでは、$\Gamma$ だけ増加する。
なお $\phi$ は、渦によって縁取られた障壁を導入することで単一値にできる。また、この障壁を横切るとポテンシャルが跳躍する。渦を生成する衝撃力は、衝撃的圧力 $-\phi$ とも見なせる、これは障壁 $S$ 上で $\Gamma$ の圧力差が作用することとも等価である。したがって:
$$
\left\{
\begin{split}
&\, \B{I} = \Gamma \int \diff \B{S} \qquad(3) \EE
&\, \B{A} = \Gamma \int \B{x} \times \diff \B{S} \qquad(4)
\end{split}
\right.
$$
ここで、$\diff \B{S}$ の方向は、右手系で取られた循環の方向とする。(1)と(2)、そして(3)と(4)の等価性は、ストークスの定理の拡張の結果とも言える。
$$
\left\{
\begin{split}
&\, \oint \psi \diff \B{s} = \int \diff \B{S}\times \nabla \psi \EE
&\, \oint \B{a}\times \diff \B{s} = \int \diff \B{S}\,\text{div} \B{A}-(\nabla \B{a})\cdot \diff \B{S}
\end{split}
\right.
$$
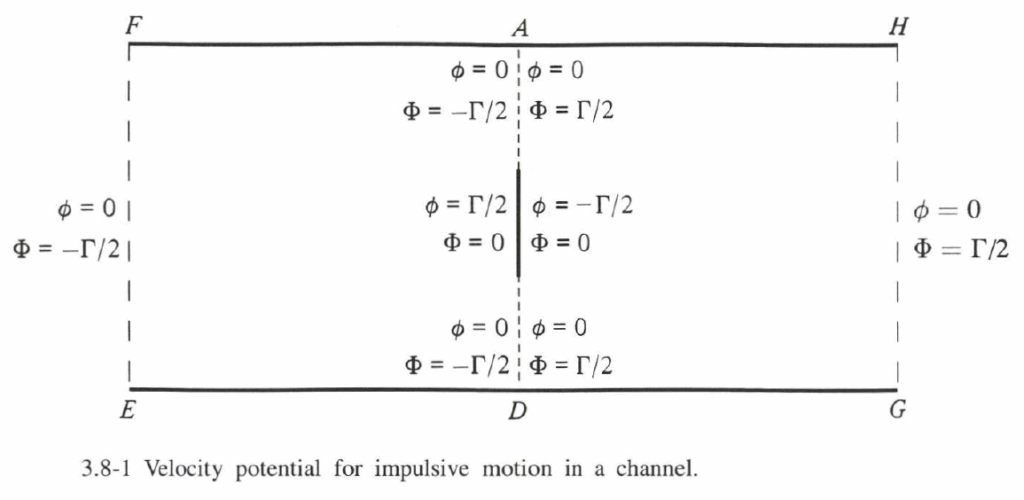
(3)の使用は、明らかにパラドックスな結果をもたらす可能性がある。例えば、軸が互いに平行で、半径 $R_0$ の管内に存在する半径 $R$ の渦輪の例を考えてみることにしよう(図3.8-1に示す)。
インパルスは軸に沿って $\pi \Gamma R^2$ で、(1)より直接または、(3)より速度ポテンシャル $\phi$ が左から右へ $-\Gamma$の跳躍を持つ、障壁BC上に適用することで得られる。速度ポテンシャルと衝撃圧力を単一値にする代替方法は、渦を壁に接続する環状障壁AB, CDを導入することである。
この障壁を横切って、速度ポテンシャル(今度は $\Phi$ で表す)は左から右へ $\Gamma$ の跳躍を持ち、インパルスは $\pi \Gamma (R^2-R^2_0)$ を与える。見かけ上のパラドックスは、$\Phi$ が無限遠で消失しないことに注意することで解決される。左側の無限遠での値 $\DL{ -\ff{1}{2}\Gamma }$ と右側での値 $\DL{ \ff{1}{2}\Gamma }$ から、寄与 $\pi \Gamma R^2_0$ が生じる。

コメント