Saffman & Szeto(1981)および Pierrehumbert & Widnall(1981)は、等しい面積 $A$ と 等しい循環 $\G$ をもつ渦斑が一直線上に並び、隣接する渦斑の中心間の距離が $L$ であるという一次元配列での性質を、等高線力学の方程式を数値積分することで調べた(図 9.7-1)。
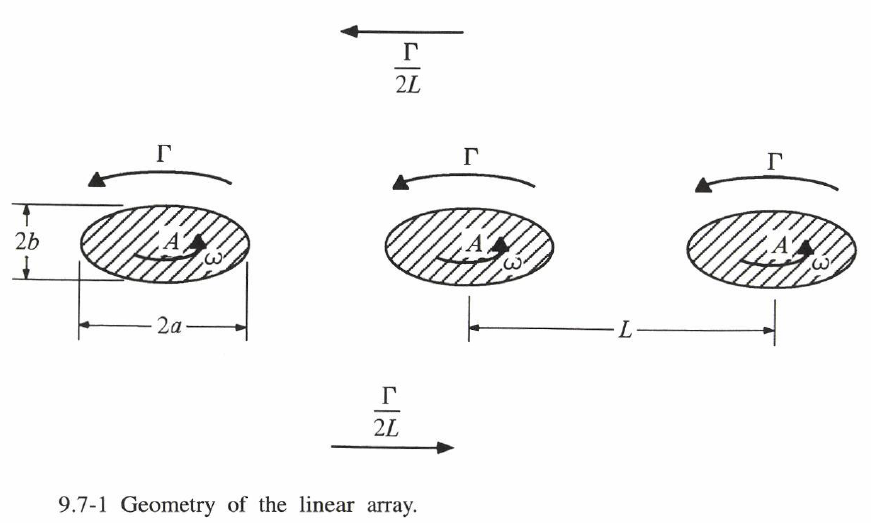
無次元量 $\alpha \equiv A/L^{2}$ を $0$ から極限値まで増やしていくと、隣接渦同士のすき間は小さくなる。小さなときの渦斑はほぼ円形だが、ギャップが大きくなると楕円状になる。この配置(形状)は $\alpha=A/L^{2}$ の関数として定まり、代表的な特性曲線が図 9.7-2 に示している。
なお、これらの結果は、渦斑が楕円対称を保つと仮定している点に注意されたい。この仮定のもとでの解は $\alpha<0.2377$ の範囲でしか存在しないが、この値はフォールド点(極限点)であって、渦斑が接触する臨界値とは限らない(数値は Kamm(1987)による)。
フォールドの存在はむしろ、同一面積を共有する近傍解(別分枝)の存在を示唆するものである。つまり、無粘性かつ時間可逆な流れにおいては、微小擾乱に対して中立モードが現れうるのである。これは通常、固有値の衝突に対応し、波長 $L$ をもつ二次元擾乱に関して安定→不安定への遷移(超調波ティアリング・モード不安定)が起こりうることを示唆しているのである(Moore & Saffman(1975a))。

他方、Kelvin の変分原理は、過剰運動エネルギーが停留(極値)となる点で安定性が切り替わることを予言している。つまり、折り目(フォールド)は、$\A$ の関数としての運動エネルギーが最大または最小となる点を表していると予想される。
さて、Saffman & Szeto の数値計算より、面積が最大のところで過剰エネルギーが最小となることが確かめられている。また、Baker(1980)は、Baker, Saffman, Sheffield(1976)が扱った空洞渦の線形配列について、この点を解析的に照合している。
ところで、渦斑が臨界値で接触すると、解の族は連結した渦の族、あるいは有限振幅の波(有限厚さ $2b$ の渦層上の波)へと連続する。厚さが一定 $2b$ の渦層が波の族へ分岐する臨界波長は $9.83b$ である(Rayleigh [1945], vol.Ⅱ, p.396)。これらの族の形状と特性は循環 $\G$ には依存しておらず、$\G$ はただ時間スケールを定めているだけである。
次に、2次元微小擾乱に対する安定性を、正規モード解析で調べることにしよう。これは §7.5 で扱った点渦の直線配列の安定性解析を、有限面積の渦へ拡張するものである。まず、乱流の流れ関数 $\Psi(x,y,t)$ は、Floquet の理論から次のように書くことができる。
$$
\begin{split}
\Psi (x,y,t) = \Psi_0(x,y)+\eps e^{\sigma t}\psi(x,y) e^{ \ff{i2\pi px}{L} }
\end{split} \qquad(1)
$$
なお、$\Psi_0(x,y)$ は非摂動時の流れ関数であり、そして $x$ の周期関数($\Psi_0(x,y)\equiv \Psi_0(x+L,y)$)$, \eps \ll 1$ かつ、 $\psi(x,y)$ は固有関数、$\sigma$ は固有値、$p$ は任意の実数定数であるとする。また、$p$ は擾乱の波数と呼ばれるものである。このとき、固有関数 $\psi(x,y)$ も $x$ について周期 $L$ の関数であると言えて、このようにできる。
$$
\begin{split}
\psi(x,y) = \sum_n^{\infty} \psi_n (y) e^{ \ff{i2\pi px}{L} }
\end{split} \qquad(2)
$$
$p$ が整数ならば、$p=0$ としても一般性を失わない。なぜなら、固有関数 $\phi_n$ の成分の付け替えにすぎないからである。この場合、擾乱は、非擾乱状態の渦と同じ波長を持ち、超調和擾乱と呼ばれる。また、すべての渦は同じように変形する。超調和擾乱の場合は、面積がゼロの極限では自明であることに注意が必要である。
一方、$p$ が整数でないときは、$0< p < 1$ としても一般性を失わない。仮に $p$ が有理数、すなわち $p=M/N$ ならば、$N$ 番目の渦が繰り返される。この外乱は分数調波と呼ばれ、特に興味深いのは、$p=\DL{\ff{1}{2}}$ の特殊なケースである。2つおきの渦も同様に変形し、波長は $2L$ となる。これは対合不安定性と呼ばれる。面積が小さな渦の場合、これは最も不安定な擾乱となる。
(1) と (2) をオイラー方程式に代入し、$\eps$ を線形代数的に近似すると、$\sigma$ の値に関する一般化固有値問題が得られ、その解は以下の形になる。
$$
\begin{split}
\sigma = \ff{\G}{L^2} \RM{fn} \left( \ff{A}{L^2}, p \right)
\end{split} \qquad(3)
$$
ここで、$\RM{fn}$ は $A/L^2>0$ のとき無限個の分岐を持つ多価関数であり、$\{\psi_n(y)\}$ の無限集合は対応する固有関数を記述する。擾乱を受けていない渦度分布が滑らかで、$\Psi_0$ も滑らかな関数である場合、一般化固有値問題は、例えばオイラー方程式の差分切断を用いて行列形式に変換することができる。
Pierrehumbert と Widnall [1982] はこの手法を用いてスチュアート渦の安定性を研究したが、渦斑には適していないことが分かっている(下記参照)。等高線動力学法は超調和擾乱には使用できるが、$p$ が小さな整数の逆数である場合を除いて、分数調和擾乱には適さない。
Schwartz 関数法は、一般の分数調波波数pの分数調波摂動に用いることができて、$\zeta$ を単位円として渦斑の境界を次のように取れる。
$$
\begin{split}
z = a_0 \zeta \left(1+\ff{a_1}{\zeta}+\ff{a_2}{\zeta^2}+\cdots \right) \qquad z^{*} = a_0^{*}\zeta (1+a_1^{*}\zeta+a_2^{*}\zeta^2+\cdots)
\end{split} \qquad(4)
$$
なお、$a_n$ と $a_n^*$ は共役複素数($\overline{a}_n = a_n^*$)にあるが、これらは独立変数であるかのように扱うことにする。次に、$\overline{z}$ についての Schwartz 分解により、渦斑によって誘起される速度の成分 $u$ と $v$ の式が得られる。($g_n$ と $g_n^*$ は $a_n$ と $a_n^*$ の解析関数)
$$
\left\{
\begin{split}
&\, u-iv = -\ff{1}{2}i\om \sum_{n=0}^{\infty} \ff{g_n}{z^n} \EE
&\, u+iv = \ff{1}{2}i\om \sum_{n=0}^{\infty} \ff{g_n^*}{z^{*n}}
\end{split} \qquad(5)
\right.
$$
適切に並進する座標系における定常平衡形状は、係数 $\{A_n\}$と $\{\overline{A}_n\}$ の集合によって記述される。例えば、$m$ 番目の渦斑の微小摂動は次の形をとる。
$$
\left\{
\begin{split}
&\, a_n^{(m)}(t) = A_n+\eps b_n^{(m)} e^{\sigma t} \EE
&\, a_n^{*(m)}(t) = \overline{A_n}+\eps b_n^{*(m)} e^{\sigma t}
\end{split} \qquad(6)
\right.
$$
上の様に、式が対称のために、さまざまな渦斑の摂動は以下の形になることが言える。($p$ は分数調波の数)
$$
\left\{
\begin{split}
&\, b_n^{(m)} = B_n e^{i2\pi pm} \EE
&\, b_n^{*(m)} = B_n^* e^{i2\pi pm}
\end{split} \qquad(7)
\right.
$$
境界条件(2.6)を $\{a_n\}$ と $\{a_n^*\}$ に対する解析的制約として表現すると、例えば $m=0$ のような渦斑の 1 つに対して、固有値 $\sigma$ と固有ベクトル $\{B_n\}, \{B_n^*\}$に対する無限線形代数的固有値問題が生じる。(定式化の詳細については、Meiron, Saffman and Schatzman [1984]およびKamm [1987]を参照。)
今は、$B_n$ と $B_n^*$ が互いに複素共役ではないという事実は問題にならない。これは、実固有値問題の固有値が複素数であることに対応するだけである。面積 $A$ が $0$ のとき、分数調波擾乱のみが関係し、$\sigma$ は式(7.5.8)で与えられる。面積が増加するにつれて、$\sigma$ の面積依存性は、代数系の打ち切りを数値的に解くか、摂動法によって求めることができる。Jimenez [1987, 1988]を参照。

図 9.7-3は、主要分数調波の成長率についての面積依存性を示している。曲線は、$\A = 0.10,0.20,0.23$ の場合と、$\A = 0.235$ の場合の折り返しを越えた最上段の枝についてプロットしている。折り返し地点を越えると、スーパーハーモニック摂動($p = 0$ または $p = 1$)は不安定になることに注意して欲しい。このクラスの分数調波摂動では、$p = \DL{\ff{1}{2}}$ のペアリング不安定性が最も不安定となる。ペアリング不安定性は定常である。つまり、$\Im \sigma = 0$ であり、擾乱は伝播しない。
超調和振動または形状振動の振動周波数に対する面積の影響を図 9.7-4に示す。$A=0$ の場合、これらは孤立した円形渦の周波数である。面積が増加すると、褶曲に対応する値で最低モードの固有値が衝突する。また、超調和-低調和摂動摂動、例えば、他のすべての渦が同じように動く形状振動も考えられる。ただし、変化はわずかである。図には $p=\DL{\ff{1}{2}}$ のときの周波数が示されている。
カルマン渦列についても同様の解析を行うことができる。特に興味深いのは、有限面積が分数調波点渦の不安定性に及ぼす影響である。各列の渦が同じ面積を持つと仮定する必要は無いが、渦の循環が等しく、向きが逆と仮定する必要がある。

また、対称的にずらされたケース、つまり各渦斑の重心が他の列の渦斑の重心の中間に位置し、さらに各渦斑が前後対称であるケースにのみ注目する。追加の幾何学的パラメータがあり、固有振動数は以下の形となる。
$$
\begin{split}
\sigma = \ff{\G}{L^2}\,\RM{fn} \left( p, \ff{A}{L^2},\ff{H}{L}, \Delta \right)
\end{split} \qquad(8)
$$
ここに $H$ は渦の列間の距離であり、これらの渦の面積は $1\pm \Delta A$ である。さらに、アスペクト比と呼ばれる $k = \DL{\ff{H}{L}}$ を導入する。ここでも、$p$ は分数調波の波数である。なお、点渦($A = 0$)の解析は§7.6 (カルマン渦列)で実施している。点渦の中立境界、すなわち $p-k$ 平面における $\Re\,\sigma=0$ となる軌跡は図7.6-1に示している。十字に注目すると、任意の $k$ に対して、摂動が不安定になる $p$ の範囲が存在するという結論が導き出される。ただし、臨界値 $k_c = \sinh^{-1}1=0.28055$ では、不安定な線形モードは存在しないのである。また、固有値は $p=\DL{\ff{1}{2}}$ について対称であることにも注意して欲しい。つまり、$\sigma(p)=\sigma(1-p)$ という関係があるのである。Meiron, Saffman, Schatzman [1984] は、交差構造が有限領域で維持されることを数値的に初めて示している。ただし、交差が2つあり、$p=\DL{\ff{1}{2}}$ を境に対称性が変化する。
Jimenez [1988] 十字クロスの中心がこのように動くことを解析的に示している。
$$
\left\{
\begin{split}
&\, k_c = 0.28055+0.55536(1+\D^2)A^2+O(A^4) \qquad(9)\EE
&\, p_c = 0.5\pm 4.63089(1+\D^2)A^2+O(A^4) \qquad(10)
\end{split}
\right.
$$
これらの値は、Meiron, Saffman, Schatzman および Kamm[1987]の数値計算結果とも整合している。Jimenez[1987]と MacKay[1987]は、この運動がハミルトニアン構造をもつことから、点渦の十字(cross)がこのような形で展開(unfold)すること、したがって有限面積を持つことは、配列(array)の安定化にも不安定化にも寄与しないことを示した。

図9.7-5(a)は、安定境界の軌跡を示している。各 $k$ について、($A$ の関数である)特別な値 $k_c$ を除けば、そのモードが不安定となるような $p$ が常に存在することに注意せよ。さらに、$k \approx k_c$ のとき、$p=\DL{\ff{1}{2}}$ のペアリング(pairing)モードが有限面積によって安定化していくことにも注意せよ。
このことは Saffman と Schatzman[1982a]によって見いだされている。ただし、ペアリング・モードが最も不安定というわけではない。図9.7-5(b) は、ある与えられた $k$ に対して成長率が $p$ にどう依存するかを示した図である。Christiansen と Zabusky は、輪郭力学(contour dynamics)方程式を数値積分することにより、サブハーモニック(subharmonic)の有限振幅擾乱が有限面積によって安定化されることを見いだした。(注24)
Dritschel[1985]は、正多角形の頂点に配置された等しい渦斑の平衡形状と安定性を計算している。Dhanak[1992]は楕円渦モデルを用いて漸近結果を得ている。渦斑ではないが、有限のコアをもつ渦の直線配列をモデル化できる、滑らかな渦度分布に対する閉形式解として、Stuart[1967]渦に触れておくのが適切であろう。特に定常(2次元・非粘性)流れでは、流れ関数 $\psi$ と渦度 $\omega$ は以下を満たす。
$$
\begin{split}
\nabla^2 \psi = -\om = F(\psi)
\end{split} \qquad(11)
$$
Stuart は特別な場合 $F(\psi)=e^{-2\psi}$ を取り、(11) が次の厳密解を持つことを見出している。
$$
\begin{split}
\psi = \log \left( C\cosh y+\sqrt{C^2-1}\cos x \right)
\end{split} \qquad(12)
$$
$C=1$ の極限では、$u=\psi_y=\tanh y$ となり、これは一様せん断層の速度分布のモデルである。もう一方の、$C\to\infty$ の極限では、以下を得る。
$$
\begin{split}
\psi \sim \log C+\log(\cosh y+\cos x)
\end{split} \qquad(13)
$$
これは、循環 $\Gamma=-4\pi$ をもち、間隔 $2\pi$ で並ぶ点渦列の流れ関数である。$C$ が $\infty$ と $1$ の間にあるとき、流線はせん断層の周期的擾乱に特徴的な“cat’s-eye(猫目)”パターンを示す。
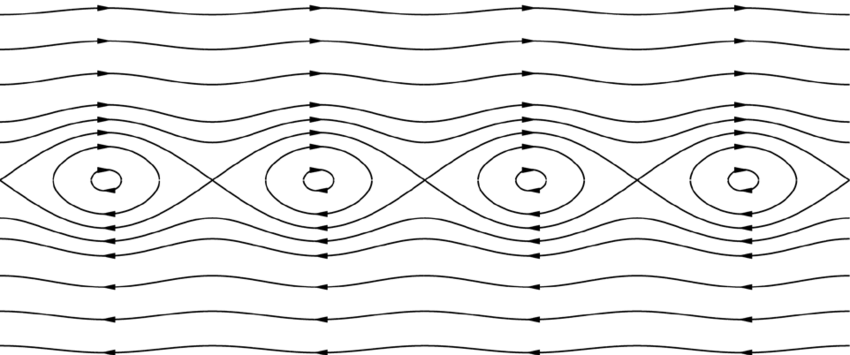
Pierrehumbert と Widnall[1982]は、これら Stuart 渦の 2次元・3次元の擾乱に対する線形安定性を計算した。2次元サブハーモニック擾乱についての結果は、渦斑の場合の結果と定性的に一致する。ペアリング・モードは常に不安定で、成長率は最大である。一方、2次元スーパーハーモニック(superharmonic)モードの挙動はこれと異なり、大きな渦ではスーパーハーモニック不安定性が存在しない。(注25)すなわち、混合層の Stuart 渦モデルではペアリングはあるが、ティアリング(tearing)はないということが言える。

コメント