等しい面積と互いに反対符号の循環をもつ反回転(counter-rotating)をしている二つの渦斑(各循環 ( $\pm\G$ )が、一定速度 $V$ で形を保ったまま等速直進する解の構造は、Deem と Zabusky(1978)によって与えられている。
さて、Pierrehumbert(1980)は、無次元パラメータ $\q = a/x_c$($a$ は各渦の半径、$2x_c$ は渦斑同士の重心間距離)を用いて解族を計算している。今、$\q << 1$ では渦はほぼ円形で、その形も変わらず、$V_0 = \G/4\pi x_c$ の速度で並進する。一方、$\q$ が増大して渦間の隙間が小さくなると、速度比 $V/V_0$ は $1$ から $0.6$ まで低下する。そして、縦横比(長さ/幅)は $1$ から $3.34$ へ増大する。そして、$\q$ の極限値は $2.16$ となる。
二つの渦斑が接触する極限流れは、数値計算の結果から存在すると考えられている。これは Sadovskii(1971)によって計算され、その後 Saffman と Tanveer(1982)が Pierrehumbert の定式化の誤りが修正されている。このときの、渦対の並進速度は $V_c = 0.16 \sqrt{S\om^2}$ で与えられている。($S$ は各渦の面積であり、$S/(\RM{length})^2$ の極限は $0.22$ である)
空洞(hollow)あるいは停滞(stagnant)渦対については、Pocklington(1895a)(あるいは Tanveer(1986)参照)が閉じた形の厳密解を与えている。これらの族では $\q \to \infty$ で縦横比が無限大に発散するため、「接触する有限極限」は現れない。
反回転渦斑対の、2次元の無限小摂動に対する安定性は、十分詳細には研究されていないが、安定であると考えられている。Keady(1985)は、変分原理に基づく存在証明を与え、同じ循環を重心位置にもつ点渦対の速度よりも、渦斑対の速度の方が小さいことを示した。
定常的に共回転する一対の渦斑は、Saffman と Szeto [1980] によって研究され、等高線力学の方程式を数値的に解いている。渦斑が離れている場合は、渦はほぼ円となる。渦斑間の距離が縮まるにつれて、渦はより変形し、最終的には接触することになる。
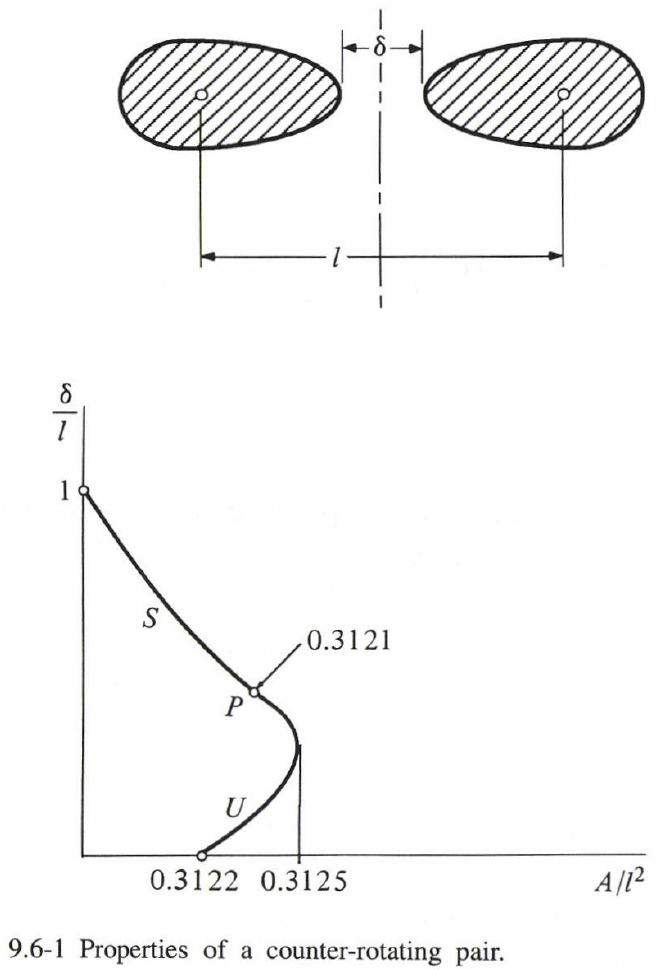
$A/l^2$ がゼロから増加すると($A$ は各渦の面積、$l$ は重心間の距離)、渦間の距離 $\delta$ は減少し、$A/l^2=0.3122$ で渦が接触する。図 9.6-1 は、$\delta/l$ を $A/l^2$ の関数として示したものである。面積の最大値、つまり渦が接触する臨界値よりも大きい値が存在することに注意して欲しい。ただし、この場合は安定性の変化とは関連していない。安定性は軌跡上の点 $P$ で変化し、$A/l^2=0.3121$ で角運動量が最小値、過剰運動エネルギーが最大値となるのである。

これを理解するにあたり、渦対の角運動量 $H$ について考えよう。とは言え、少しテクニックを用いて、以下の無次元角運動量 $\widetilde{J}$ を定義して、これについて考えることとしよう。
$$
\begin{split}
\widetilde{J} = -\ff{H}{\G A}
\end{split} \qquad(1)
$$
実際の運動エネルギーは無限大であるが、過剰な運動エネルギー $T$ を次のように定義することができる。
$$
\begin{split}
T = \iint \om\,\psi\,\diff x\,\diff y
\end{split} \qquad(2)
$$
なお、流れ関数 $\psi$ は、$r→\infty$ にて $\psi \sim \DL{ -\ff{\G}{\pi}\log r+O(1) }$ と漸近するという要件によって正規化される。すなわち、無次元過剰エネルギーは、このようになる。
$$
\begin{split}
\widetilde{T} = \ff{T}{\G^2}
\end{split} \qquad(3)
$$
無次元角運動量は、$A/l^2= 0$ のとき無限大となり、$A/l^2=0.3121$ のとき最小値まで減少し、その後、渦が接触するまで増加する。$\widetilde{T}$ についても同様の挙動が成り立つが、最初は増加し、その後減少する。$\widetilde{J}$ の最小値と $\widetilde{T}$ の最大値(図 9.6-2 参照)は、$A/l^2$ の値が同じときに発生する。これは、ケルビンの変分原理の結果であり、この値で 2 次元微小擾乱に対する安定性が変化することを意味する。なぜなら、下側の枝が最小値であれば、上側の枝は最小値ではなく、したがって不安定になるからである。これは、Kamm による逆回転渦対の線形安定性の計算と一致している。渦が接触した後、形状はキルヒホッフの楕円渦の分岐から生じる単連結渦が、単一のダンベル形状で接続されると予想される。
接触渦の正確な閉形式解は、Lamb [1932 $165]によって与えられている。これは、渦度が均一でない場合のものである。具体的には、半径 $a$ の円筒内を流れる速度 $U$ の 2 次元定常流を考えており、円筒には渦度分布 $\om(r,\q)$ が存在しているとする。ここに、$r$ と $\q$ は円筒座標系であるとする。さて、$r > a$ の場合、流れ関数 $\psi$ はこのようになる。
$$
\begin{split}
\psi = -U\left( r-\ff{a^2}{r} \right)\sin\q
\end{split} \qquad(4)
$$
円筒内部に定常流があるとき、$f$ を任意関数とし、$\om = -\nabla^2 \psi = f(\psi)\,\,\, (r<a)$ とできて、さらに、$k$ を定数として $f(\psi) = -k^2\psi$ と置く。このとき、
$$
\begin{split}
\ff{\del^2 \psi}{\del r^2}+\ff{1}{r}\ff{\del \psi}{\del \q^2}+\ff{1}{r^2}\ff{\del^2 \psi}{\del \q^2} = -k^2\psi
\end{split} \qquad(5)
$$
という方程式が得られる。この方程式は、次のような解を持つ。($J$ はベッセル関数)
$$
\begin{split}
\psi = C\, J_1(kr)\sin\q, \quad \om = -Ck^2\, J_1(kr)\sin \q
\end{split} \qquad(6)
$$
今、$r=a$ にて $\psi$ と $\DL{ \ff{\del \psi}{\del r} }$ が連続となるように $C$ と $k$ を選ぶと、以下が得られる。
$$
\begin{split}
J_1(ka) = 0, \quad C = -\ff{2U}{k\,J_0(ka)}
\end{split} \qquad(7)
$$
この解に一様流速度 $U$ を重ね合わせると、無限空間の流体中を一定速で進行する渦が得られる。この渦のインパルスは、
$$
\begin{split}
\iint y\,\om\,r\,\diff r\,\diff\q = -Ck^2\pi \int_0^a r^2\,J_1(kr)\,\diff r = 2\pi a^2 U
\end{split} \qquad(8)
$$
となる。さらに D. Bliss(1970, private communication)は、Lamb の解が円運動する接触渦対にも一般化できることを指摘している。すなわち内部 $r<a$ において、
$$
\left\{
\begin{split}
&\, \psi = Ur\sin\q+CJ_1(kr)\sin\q+BJ_0(kr)-\ff{Dr^2}{4} \EE
&\, \om = Ck^2J_1(kr)\sin\q+Bk^2J_0(kr)+D
\end{split}
\right. \qquad(9)
$$
となって、明らかに $\om = -\nabla^2 \psi$ が成立する。そして、外部 $r>a$ においてはそれぞれ、
$$
\left\{
\begin{split}
&\, \psi = \ff{Ua^2}{r}\sin\q-\ff{Da^2}{2}\log r \EE
&\, \om = 0
\end{split}
\right. \qquad(10)
$$
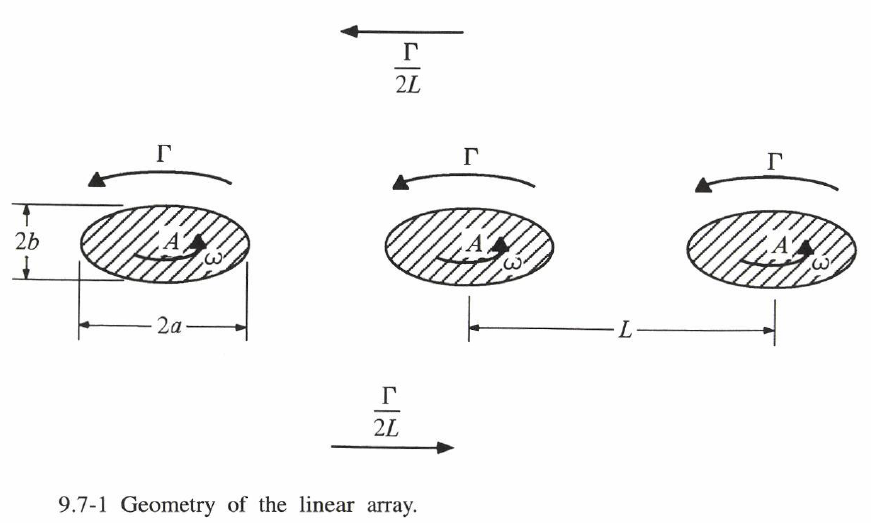
ここで、これが円境界 $r=a$ の中心が、角速度 $\Omega$ と速度 $U=b\Omega$ を持つ半径 $b$ の円を描く運動を記述していることを証明しよう。まず、式(9)から、$\om$ は $r=a$ 上で一定であることが分かり、そして、速度成分 $\del \psi/\del \q$ と$\del \psi/\del r$はr=a上で連続であることが言える。
最終的なゴールは、$\DL{\ff{D\om}{D t}=0}$ を示すことである。今、
$$
\left\{
\begin{split}
&\, \ff{\del r}{\del t} = -U\cos\q \EE
&\, \ff{\del \q}{\del t} = \ff{U\sin\q}{r}-\Omega
\end{split}
\right. \qquad(11)
$$
円を中心とする極座標の場合。直接代入すると、$D=\Omega$ は渦度保存則を満たすことが分かる。興味深いことに、この解は $B$ には依存していない。

コメント