保存力または境界運動により、静止状態から始動する非粘性非圧縮流体の物体周りの流れを考えよう。この流れが連続でない限り運動は一意とはならない。この場合、ヘルムホルツ-ケルビンの定理は、流れ内の渦度がゼロで、速度が単一値ポテンシャルの勾配であることを示す。不連続流れが許される場合、例えば渦層が物体から流体に入ることを許すなら、完全流体の非定常流は一意解を持たない。
それ自身に垂直に運動する平板により生成される流れを考える。一意なポテンシャル流解は、§1でKaffeelöffel 実験との関連で議論したものである。この流れは流体内のすべての点で連続である。図6.6-1(a)に示すように、代替案は鋭い縁から発生する渦層を伴う分離流れである(Anton [1939])。速度場は連続でない。
第二の例は、管からの流出である。ポテンシャル流が存在するか、または流れが管縁で分離し、渦輪に巻き上がる渦層が現れる(図6.6-1(b)参照)。第三の例は、翼型周りの開始流れである。連続ポテンシャル流を図6.7-1(a)下に示す。図6.6-1(c)は後縁を離れる渦シートと前縁での分離泡を伴う分離流れを示す。

ポテンシャル流れは連続だが有界でなく、鋭い縁では速度が無限となる。一方、分離流れは不連続だが速度は有界である。これらは $ν → 0$, $t$ 固定でのナビエ・ストークス方程式解の極限である可能性が高いと推測される。しかし純粋に非粘性理論の枠組み内では流れ間の選択方法はない。
さらに、図6.6-2にスケッチしたように、分離点に依存する無限の方法で滑らかな物体周りの流れに対して分離が起こらない既知の理由はなく、各流れはオイラー方程式の解であるという意味である。
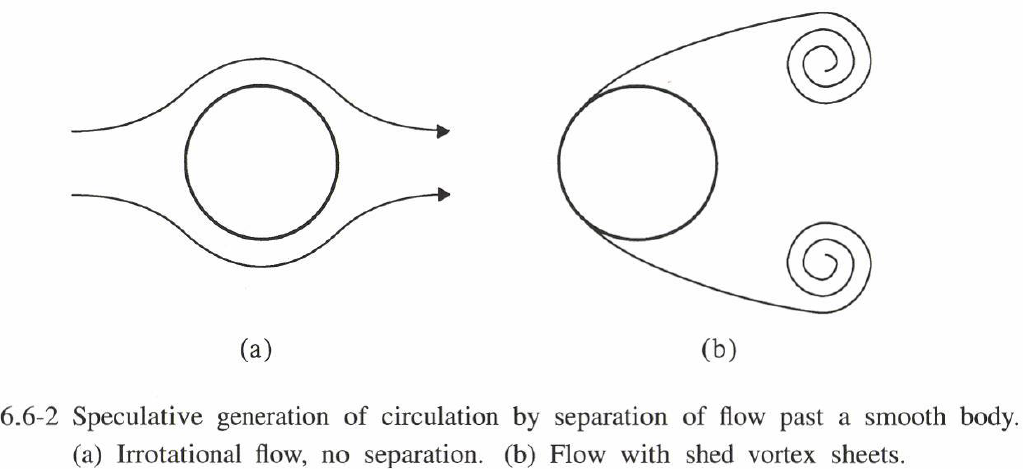
渦層の流れ分離による創造は、ヘルムホルツ-ケルビンの定理に違反しない。渦層は無限に薄く、$t = 0$ で流体内にあった流体粒子を含れず、渦度は完全に境界から来る。
また、$t = 0$ で流体内に完全に存在する物質回路周りの循環は全ての $t > 0$ でゼロである。流体内に完全に存在する回路周りに循環が現れ得るが、これらの回路は初期物質回路の発展ではない。物体周りの定常流れに対して、渦度分布に依存するオイラー方程式の明らかに無限多の可能解があるためである(例えば、有限サイズ渦を持つFöppl型流れ)。

コメント