一様定常な渦斑の厳密解について知られているのは、Kirchhoff 渦と Moore-Saffman 渦を一般化したもののみである。数値計算による解法としては、等高線力学ないしはシュワルツ関数によるアプローチを用いて、様々な配置での平衡形が調べられてきた。
まずは、静止流体中にて単一の渦斑が回転する場合について考える。Deen と Zabusky [1978] が述べたように、Kirchhoff 渦は、$n$ 多角形対称性を持つような、無限に存在する回転渦族の 1 つの例($n=2$)に過ぎない。実際、これらの解の存在は、分岐解析によって容易に証明される。今、半径 $a$ 渦度 $\om$ の均一な円形渦斑に対する $n$ 回対称性の微小(2次元)擾乱を考える。(Kelvin [1880], Larnb [1932, §158], Batchelor [1967 §7.3]) 境界の変形を伴う。この変形は渦度(および面積)を一定に保ち、その境界は($\delta << 1, n \neq 0$)の形状をとる。この前提の下では、渦斑の半径 $r$ の時間変化はこのように表せる。
$$
\begin{split}
r = a(1+\delta e^{i(n\q-\sigma t)})
\end{split} \qquad(1)
$$
そして、渦斑内外の流れ関数 $\psi$ はこのようになる。
$$
\psi =
\left\{
\begin{split}
&\, \ff{1}{4}\om (a^2-r^2)+A\delta \ff{r^{|n|}}{a^{|n|}}e^{i(n\q-\sigma t)} \quad (r<a) \qquad(2) \EE
&\, -\ff{\om a^2}{2} \log \left( \ff{r}{a} \right)+B\delta \left( \ff{a}{r} \right)^{|n|} e^{i(n\q-\sigma t)} \quad (r>a) \qquad(3)
\end{split}
\right.
$$
関数の具体的な形は、擾乱が非回転的であるという条件によって決定される。具体的には、$σ, A, B$ の値は、変形境界 (1 )が、$ψ$ と $\nabla \psi$(要するに $p$ )が連続する物質表面であるという条件から導かれる。$\delta^2$ のオーダーの項を無視すると、次式が得られる。
$$
\begin{split}
&\,A =B = -\left( \sigma9\ff{1}{2}|n|\,\om \right) \qquad(4) \EE
&\, \sigma = \ff{1}{2}\om\big( |n|-1 \big)\,\RM{sgn}\,n \qquad(5)
\end{split}
$$
$n = \pm 1$ は渦斑が形を変えずに移動するような自明の解となる。そして、擾乱による角速度 $\Omega_n$ は $\sigma/n$ である。つまり、
$$
\begin{split}
\Omega_n = \ff{1}{2}\om\left( 1-\ff{1}{|n|} \right) \qquad(6)
\end{split}
$$
となる。
乱されていない領域内の流体は角速度 $1/2ω$ で剛体回転しているため、乱れは流体に対して後方に移動していく。
角速度 $Ω_n$ で回転する座標系では、乱れは静止しているように振舞う。ここで、一定の面積と渦度を持ち、角速度 $Ω$ で回転する座標系で静止している経路の形状を決定する、非線形問題について考えてみることにする。これは、無限の方程式の集合としてこのように表現できる。
$$
\begin{split}
N(a_n; \Omega) = 0
\end{split} \qquad (7)
$$
ここで未知数は、境界についてのフーリエ級数の係数の無限集合 $\{a_n\}$ であり、以下の形を取る。
$$
\begin{split}
r = a+\sum_{-\infty}^{\infty} a_n\,e^{in\q}
\end{split} \qquad (8)
$$
ただし、$a_n = \overline{a}_{-n}$ と $\Omega$ は制御パラメーターとして見なされる。
全ての $\Omega$ に対して、自明解 $\{a_n\} = 0$ が存在している。$Ω=Ω_n$ の無限小解の存在は、$Ω$ が $Ω_n$ の値を通過するときに分岐が存在することを示唆している(図 9.4-1参照)。これは直接的な解析によって検証できる。例えば、Su [1979] は、$m$ 重対称族への分岐の結果について、
$$
\begin{split}
r = a\left( 1-\ff{1}{2}\delta^2 \right)+\delta \cos m\q+\ff{2m-1}{4}\delta^2 \cos 2m\q+\cdots
\end{split} \qquad (9)
$$
そして、
$$
\begin{split}
\Omega = \Omega_m \left\{ 1-\ff{\pi \delta^2}{4}(m-1)+\cdots\,\,\right\}
\end{split} \qquad (10)
$$
であることを示している。なお、$m=2$ としたとき、円に近い Kirchhoff 渦の公式の結果に一致する。
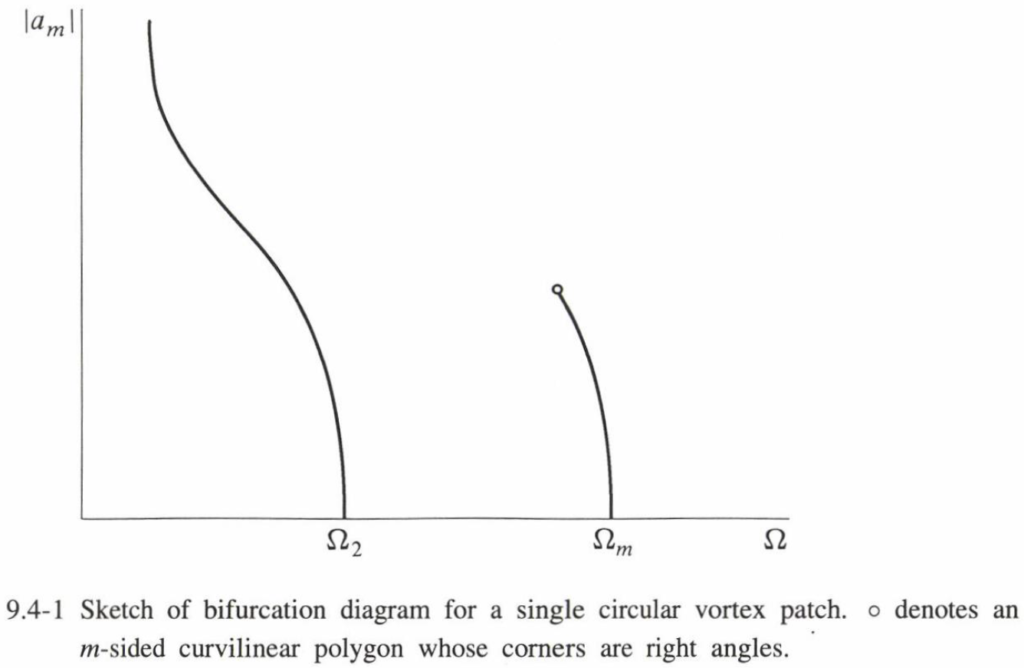
Deem と Zabusky の数値解析によると、各枝( $m>2$ の場合)は曲線多角形で終わる。Saffman と Szeto [1980]による渦斑の角の形状解析では、夾角は $90°$ で曲率は無限大であることが示された。頂点における接線は、頂点における対称軸に沿って $\q=0$ としたとき、局所極座標にて次式で表される。
$$
\begin{split}
\q’ = \pm\left( \ff{1}{4}\pi+\ff{\pi}{8}\log r’+O\left( \ff{1}{\log r’} \right) \right)
\end{split} \qquad (11)
$$
渦斑は最初、線形安定であるが、さらに分岐して対称性が低い形状になる可能性も否定できない。 Kirchhoff 渦の $m = 2$ の場合の明示的な計算は、Moore と Saffman [1971] によって行われている。彼らは楕円曲線座標を用いた計算によって、Kirchhoff 渦に対する $m$ 重対称擾乱の固有周波数 $\sigma$ が次式で与えられることを示した。
$$
\begin{split}
\sigma^2 = \ff{1}{4}\om^2 \ff{(a^2+b^2)^2}{(a+b)^4}\left[ \left\{ \ff{2mab}{a^2+b^2}-\ff{(a+b)^2}{a^2+b^2} \right\}^2-\ff{(a+b)^4}{(a^2+b^2)^2}\left( \ff{a-b}{a+b} \right)^{2m} \right]
\end{split} \qquad (12)
$$
ここに $a,b$ は楕円の長軸と短軸を表すとする。$\DL{\ff{a}{b}<3}$ のとき、$\sigma^2>0$ となることが示される。$m=2$ のモードは、$\DL{\ff{a}{b}=3}$ のとき安定性の交換によって不安定になる(Love [1893])。このとき、対称性のない渦斑の族への分岐が生じるが、これらの渦斑は(少なくとも分岐点近傍では)2重対称擾乱に対して不安定である。
さらなる分岐は、$m$ の他の値では $\sigma$ がゼロになる、つまり、 $\DL{\ff{a}{b}}$ の値で発生する。Kamm [1987] はこれらの特性を詳細に研究している。Moore と Saffman [1971] もまた、$3 で記述した歪んだ楕円渦の 2 次元微小擾乱の安定性特性を研究している。この場合、以下のようになる。
$$
\begin{split}
\sigma^2 = \ff{\om^2}{4}\left\{ \left( \ff{2mab}{a^2+b^2}-1 \right)^2-\left( \ff{a-b}{a+b} \right)^{2m} \right\}
\end{split} \qquad (13)
$$
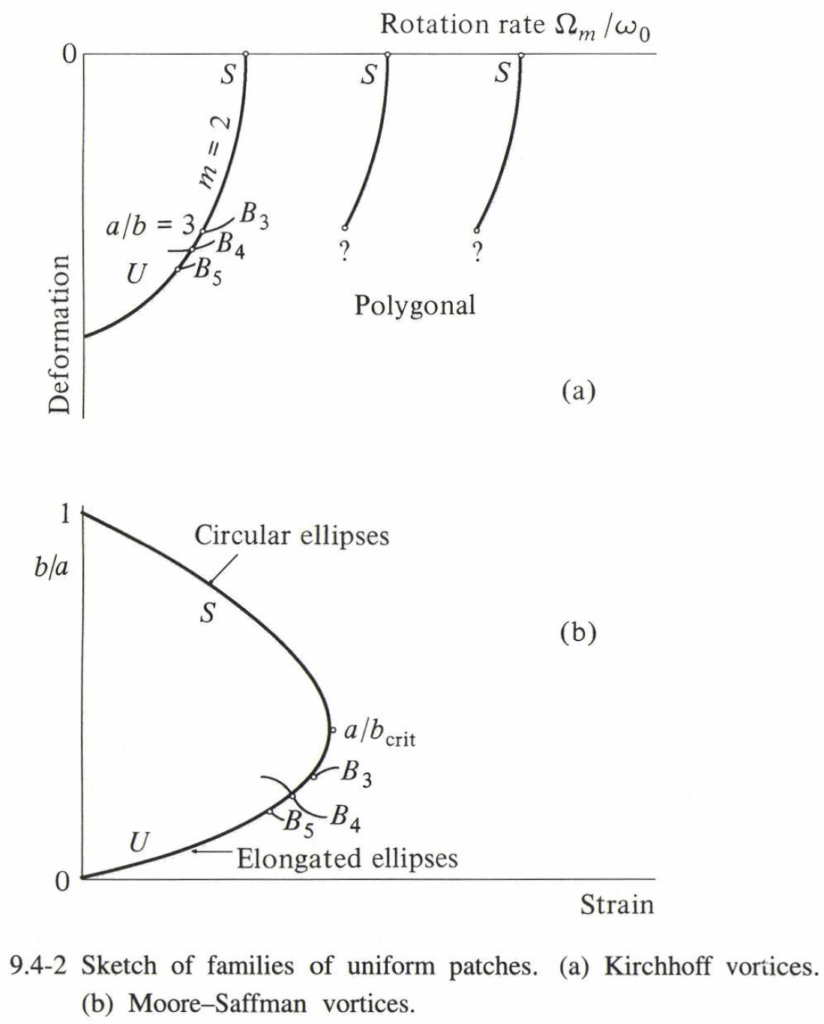
したがって、歪んだ楕円渦は、$a/b<(a/b)_c$ の場合には線形安定であり、それ以外の場合には不安定となる。$a/b$ の値において $\sigma=0$ かつ $m>2$ となるような値では、非楕円渦の族への分岐が生じる。これらは Kamm [1987] によっても研究されている。図 9.4-2 は、存在し得る解の族のいくつかを模式的に示すものである。
ここで論じる不安定性は安定性の交換であり、固有値の2乗である $\sigma^2$ の符号の変化に対応している。不安定性は固有値の衝突によっても発生する可能性がある。例えば、$\sigma_{m1}$ と $\sigma_{m2}$ が異なるモードまたは固有関数に対応する2つの周波数であり、制御パラメータのある値(例えば $a/b$ )に対して $\sigma_{m1}=\sigma_{m2}$ である場合、不安定性のバブル、つまり周波数(固有値)が複素数で定常状態が不安定になる制御パラメータの範囲が発生する可能性がある。これは、モードが反対のシグネチャを持つ場合に発生し、これは摂動の過剰エネルギーとして解釈できる(MacKay and Saffman [1986]を参照)。
単純せん断 $u=\kappa y$ における渦度 $\om$ の渦斑について、Moore と Saffman [1971]は、共回転する構成において、$|\kappa/\om|<1$ のとき $\kappa$ と $\om$ が逆符号となる定常解が1つ存在することを発見した。この条件が満たされない場合、楕円形の解は存在しない。渦斑の外側の渦度は $-\kappa$、渦斑の内側の渦度は $\om$ であり、軸比は以下の関係を満たす。
$$
\begin{split}
\left| \ff{\kappa}{\om} \right| (a^2+b^2) = a^2-ab
\end{split} \qquad (14)
$$
渦斑は、その長軸がせん断流線と平行になるように配向されており、微小な2次元擾乱に対して安定であることが示される。$|κ/ω|>1$ の場合、楕円形の定常解は存在しない。$κ$ と $ω$ が正負同値である逆回転配置については、$κ/ω<\DL{\ff{\sqrt{2}-1}{2} }$ の場合、2つの楕円解が存在し、変形の少ない方が安定する。$κ/ω$ がこの臨界値より大きい場合、楕円形の解は存在しない。逆回転渦斑は、長軸がせん断流の方向に垂直になるように配向されている。このとき軸比は、次式の関係を満たす。
$$
\begin{split}
\ff{\kappa}{\om}(a^2+b^2) = ab-b^2
\end{split} \qquad (15)
$$
一般的に、外部流れの詳細に応じて、楕円形の定常解は0、1、2、または3個存在し、線形2次元擾乱に対して安定または不安定となる可能性がある。

コメント