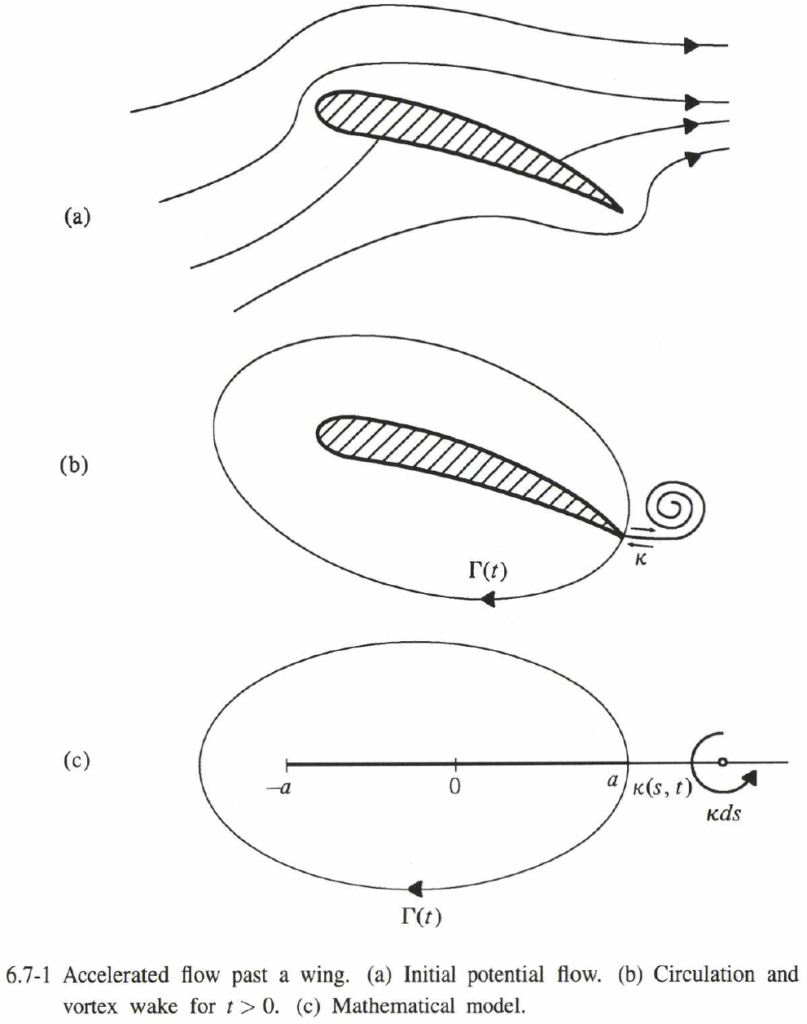
鋭い縁を持つ物体の場合、オイラー流れの非一意性は、速度が有界であることを要求するが、必ずしも連続でないKutta 条件の設定により除去できる。
二次元翼型の運動開始問題(Wagner [1925], Sedov [1965], Karman and Burgers [1934])を考え、翼周りの循環 $Γ$ の成長を計算する。問題は、後縁から放出される渦層の巻き上がりが無視でき、渦シートが自由流で対流されるという近似で解析できる。
簡単のため、小迎え角 $α$ で一定速度 $V$ で瞬間的に設定された長さ $c = 2a$ の平板を考える(図6.7-1参照)。時刻 $t$ で翼周りの循環は $Γ(t)$、渦層は強度 $κ(s,t)$ を持ち、$s$ は後縁からの距離とする。渦層の自己誘導運動が無視できるという仮定の下では、渦層強度は以下の方程式を満たす。
$$
\begin{split}
\ff{\del \kappa}{\del t}+V\ff{\del \kappa}{\del s} = 0
\end{split} \qquad(1)
$$
翼と渦層周りの全循環の保存則より、
$$
\begin{split}
\ff{\diff \Gamma}{\diff t}-V\,\kappa(0,t) = 0, \quad \text{or} \quad \Gamma = \int_0^{V_t} \kappa(s,t)\,\diff s
\end{split} \qquad(2)
$$
流れを求めるためには、二つのポテンシャル流問題を解く必要がある。第1は迎え角 $α$ での一様流れ $V$ 中の平板周りの流れである(Batchelor [1967 §6.7]参照)。複素ポテンシャルは(§7.2参照)このようになる。
$$
\begin{split}
w = \ff{1}{2}V\left\{ \zeta e^{-i\A}+\left( \ff{a^2}{\zeta} \right)e^{i\A} \right\}+i \ff{\gamma_0}{2\pi} \log \zeta
\end{split} \qquad(3)
$$
ここに、$\zeta = z+\sqrt{z^2-a^2} $ かつ、$\gamma_0$(実数)は、平板周りの循環とする。また、平板 $ -a < \text{Re}(z) < a$ は、円 $|\zeta| = a$ に写像される。
第二のポテンシャル問題は、点 $(s + a, 0)$ での強度 $κds$ の線渦により誘導される流れである。これは、
$$
\begin{split}
w = \ff{i\diff s}{2\pi} \left[ -\kappa \log\big\{ \zeta-(s+a+\sqrt{s^2+2as}) \big\}+\gamma_1\log \zeta+\kappa\log \left\{ \zeta-\ff{a^2}{s+a+\sqrt{s^2+2as}} \right\} \right]
\end{split} \qquad(4)
$$
で表される。ここに、$\gamma_1$(実数)は、時間の関数であるとする。渦層の微小要素 $\diff s$ により翼周りに誘導される循環は $-(κ + γ₁)\diff s$ と表される。
束縛循環は翼周りで Kutta 条件の設定から決定される。具体的には、$\DL{ u-iv = \left( \ff{\diff w}{\diff \zeta} \right)\left( \ff{\diff \zeta}{\diff z} \right) }$ で、$z = a$ では $\DL{ \ff{\diff \zeta}{\diff z} = ∞}$ であるため、後縁での有限速度の条件は $ζ = a$ で $\DL{ \ff{\diff w}{\diff \zeta} = 0}$ を要求する。(3)から、
$$
\begin{split}
\gamma_0 = 2\pi a V \sin\A \sim \pi V c \A
\end{split} \qquad(5)
$$
が得られて、式(4)より、
$$
\begin{split}
\gamma_1 = -\kappa \sqrt{ \ff{s+c}{s} }
\end{split} \qquad(6)
$$
と言える。そして、時刻 $t$ での翼内部の全束縛渦度 $-Γ(t)$ は、ここに、
$$
\begin{split}
\Gamma (t) = \gamma_0+\int_0^{V_t} (\kappa+\gamma_1)\diff s
\end{split} \qquad(7)
$$
と表せる。
さらに、(2)を用いて、
$$
\begin{split}
\gamma_0 = V\pi c \A = -\int_0^{V_t} \gamma_1\,\diff s = \int_0^{V_t} \kappa \sqrt{ \ff{s+c}{s}}\, \diff s
\end{split} \qquad(8)
$$
となって、今、(1)より、$\kappa = K(Vt-s)$ と言えて、$\sigma = Vt-s$ と置いて、(8)の変数を変更すると、
$$
\begin{split}
V\pi c \A = \int_0^{V_t} K(\sigma) \sqrt{ \ff{Vt+c-\sigma}{Vt-\sigma} } \, \diff \sigma
\end{split} \qquad(9)
$$
これは渦層強度 $K(σ)$ に対する Volterra 積分方程式である。$K(0)$ は渦層端の値で、$K(Vt)$ は後縁での値である。(9)の形式解はラプラス変換を用いて容易に得られる。
$$
\begin{split}
\ff{V\pi c \A}{p} = \widetilde{K}(p) \overline{\left( \ff{\sigma+c}{\sigma} \right)^{1/2}}
\end{split} \qquad(10)
$$
ここに、上付きバーは $σ$ に関する変数 $p$ でのラプラス変換を表すとする。また、$\widetilde{K}(p) = \overline{K(σ)}$ と書いている。
正確な逆変換は不可能だが、小時間と大時間に対して漸近技法を用いることはできる。小時間の場合は、$σ$ は小さく、比較して大きな $p$ に対する変換の形に興味がある。すると、
$$
\begin{split}
\overline{\left( \ff{\sigma+c}{\sigma} \right)^{1/2}} \sim c^{1/2} \int_0^{\infty} \ff{ e^{-p\sigma} }{ \sigma^{1/2} }\,\diff \sigma = \sqrt{ \ff{\pi c}{p} }
\end{split} \qquad(11)
$$
上より、
$$
\begin{split}
\widetilde{K}(p) \sim V\A \sqrt{ \ff{\pi c}{p} }
\end{split} \qquad(12)
$$
が得られる。これはさらに、
$$
\begin{split}
K(\sigma) \sim V\A \sqrt{ \ff{c}{\sigma} } \,\,\,\,\text{i.e.}\,\,\,\, \kappa(s,t)\sim V\A\sqrt{ \ff{c}{Vt-s} }
\end{split} \qquad(13)
$$
であることを意味する。渦層端での、平方根で表される特異性に注意されたい。そして、循環 $\Gamma(t)$ は(2)より、
$$
\begin{split}
\Gamma \sim 2V\A\sqrt{cVt}
\end{split} \qquad(14)
$$
で与えられる。したがって、初期には時間の平方根に比例して増加する。
一方、大きなスパンでの時間では、小さな $p$ の振る舞いに興味がある。つまり、
$$
\begin{split}
\int_0^{\infty} \sqrt{ 1+\ff{c}{\sigma} }\, e^{-p\sigma}\,\diff \sigma \sim \ff{1}{p} \big[ 1+p \log (pc) \big]
\end{split} \qquad(15)
$$
および、
$$
\begin{split}
\widetilde{K}(p) \sim V\pi c \A \big[ 1-p \log (pc) \big]
\end{split} \qquad(16)
$$
これより、極限での循環 $Γ_{∞}$ as $t → ∞$ は、
$$
\begin{split}
Γ_{∞} = \int_0^{\infty} K(\sigma)\,\diff \sigma = \widetilde{K}(0) = V\pi c \A
\end{split} \qquad(17)
$$
となることが言える。
Wagnerのラプラス変換の近似逆変換は、$t = 7c/V$ のとき $Γ = 0.9Γ_{∞}$ を示す。
翼の揚力と抗力は、圧力評価のためにポテンシャル流に対するベルヌーイ方程式の非定常形を用いることで(前縁での吸引を考慮に入れて)求めることができるが、この問題を渦力と束縛渦度の例として用いることにしよう。翼内束縛渦度のインパルス( $\DL{\int_W}$ は翼内での積分、$\DL{ \oint_W }$ は翼周りでの積分を表す)は、以下で表される。
$$
\begin{split}
\B{I} = \int_W \om\,\B{r}\times \B{k}\,\diff S
\end{split} \qquad(18)
$$
すると、
$$
\begin{split}
\ff{\diff \B{I}}{\diff t} &= \int_W\ff{\del \om}{\del t}\,\B{r}\times \B{k}\,\diff S \EE
&= \int_W \B{F}\,\diff S-\int_W (\B{r}\times \B{k})(\B{u}\cdot \nabla \om)\diff S+\oint_W(\B{r}\times \B{k})(\B{n}\times \B{F}\cdot \B{k})\diff s \EE
&= -\B{D}+\int_W \B{u}\times \B{k}\,\om \,\diff S+\oint_W (\B{u}\cdot \B{n})(\B{k}\times \B{r})\om\,\diff s
\end{split} \qquad(19)
$$
部分積分以降の式は、$\B{F}$ が翼表面で(3.7.4)を満たすことを要求し、ここで $-\B{D}$ は翼を静止保持に必要な外力で $\B{D}$ は流体により物体に加えられる力、$\B{F}×\B{n}$ は翼境界でゼロとなる。(19)の最後の項は、翼から渦層への渦度流出のため一般には消失しないが、原点を翼後縁に選ぶことでこの項を消失させることができる。すると抗力は、
$$
\begin{split}
\B{D} = \int_W \B{u}\times \B{k}\,\om\,\diff S-\ff{\diff \B{I}}{\diff t}
\end{split} \qquad(20)
$$
と表される。
(20)の右辺第一項は渦力である。自由流からの寄与は自由流に垂直な方向への揚力 $VΓ(t)$ を与える。後流渦度により誘導される速度からの渦力への寄与は、自由流に平行な $O(α²)$ オーダーの成分を与える。これは後流渦系での運動エネルギー生成に関連する「誘導抗力」である。
(20)の最後の項を計算することが残っている。後流渦度の像である束縛渦度と Kutta 条件により誘導される束縛渦度からの寄与がある。(自由流により誘導される束縛渦度は一定である。)まずは、後流渦度の像を考える。(18)より、揚力に寄与する $y$ 成分は、
$$
\begin{split}
I_y^T = -\int_{-a}^ax \left[ \int\om\,\diff y \right]\diff x = \int_{-a}^a x \big[ u(x, 0+)-u(x,0-) \big]\diff x = -\oint_W xu\,\diff x
\end{split} \qquad(21)
$$
ここに、$u$ は後流渦度により誘導される速度で、$γ_1 = -κ$ として、システム全体の渦度がゼロとなるように(4)により与えられる。このとき、原点の位置は重要でない。さらに翼上で、$\DL{ u = \ff{\diff w}{\diff z}, x = z, \diff x = \diff z}$ で、後流要素 $κ\diff s$ からの寄与 $δI_y^T$ は、以下のように表される。
$$
\begin{split}
\ff{\del I_y^T}{\kappa \diff s} &= -\oint z\ff{\diff w}{\diff z} = \oint \ff{1}{2} \left( \zeta+\ff{a^2}{\zeta} \right)\ff{\diff w}{\diff \zeta}\,\diff \zeta \EE
&= \oint \zeta \ff{\diff w}{\diff \zeta}\,\diff \zeta \quad\,\, \text{since}\,\, \diff w\,\, \text{is real and}\,\, \text{Re}\,\zeta = \text{Re}\left( \ff{a^2}{\zeta} \right) \EE
&= \ff{i}{2\pi} \oint \left( \ff{\zeta}{\zeta-r_1}-\ff{\zeta}{\zeta-r_2}+1 \right)\diff \zeta \quad\,\, r_{1,2} = s+a\pm \sqrt{s^2+2as} \EE
&= s+a-\sqrt{s^2+2as}
\end{split} \qquad(22)
$$
したがって、
$$
\begin{split}
I_y^T = \int_0^{V_t} \kappa(s,t)\big( s+a-\sqrt{s^2+2as} \big)\diff s
\end{split} \qquad(23)
$$
最後に、Kutta 条件により誘導される循環 $Γ(t)$ を持つ束縛渦度からの寄与がある。原点が後縁にあることを考慮すると、
$$
\begin{split}
I_y^K = \int_{-a}^a \left[ \int \om\,\diff y \right] (a-x)\,\diff x = \oint u(a-x)\diff x = -\Gamma a
\end{split} \qquad(24)
$$
が得られる。さらに、$\DL{ u=\ff{\Gamma}{2\pi a \sin\q} }$ のとき、式(2)と(23), (24)より、
$$
\begin{split}
I_y = \int_0^{V_t} \kappa(s,t)\big( s+a-\sqrt{s^2+sc} \big)\diff s+const.
\end{split} \qquad(25)
$$
ここに、$κ(s,t) = K(Vt – s)$ である。時間に関して微分し、部分積分すると以下を得る。
$$
\begin{split}
\ff{\diff I_y}{\diff t} = \int_0^{V_t} K(\sigma) \left[ V-\ff{V^2 t-\sigma V+\ff{1}{2}Vc }{ \sqrt{ V^2t^2-2\sigma Vt+\sigma^2+Vtc-\sigma c } } \right]\diff \sigma
\end{split} \qquad(26)
$$
なお、$\to 0$ as $t \to \infty$ さらに、$D \to \pi V^2 \A c$ である。
小さな $t$ に対して、(25)と(13)を用いると、
$$
\begin{split}
I_y \sim -\int_0^{V_t} \kappa \sqrt{sc}\,\diff s = -\int_0^{V_t} V\A c \sqrt{ \ff{s}{Vt-s} }\, \diff s = -\ff{1}{2}\pi V^2 \A ct
\end{split} \qquad(27)
$$
(20)より $Γ(0) = 0$ であるため、揚力 $L$ はこのように表せる。
$$
\begin{split}
L = \ff{1}{2} \pi V^2 \A c \quad \text{as}\quad t\to 0
\end{split} \qquad(28)
$$
したがって、衝撃的に生成された運動に対して、翼の初期揚力は最終揚力の半分となる。この挙動(Wagner効果と呼ばれる)はWalker [1931]により実験的に検証されている。最終揚力には $O(c/V)$ オーダーの時間後に到達される。また、放出された渦度はその後開始渦に巻き上がる。
翼が突然停止すると、Kutta 条件は違反され、翼周りの循環がゼロに減少するまで渦度が放出される。この後流渦度は終了渦に巻き上がる。$t → ∞$ として、開始と終了渦は飛行時間にわたって積分された、揚力に等しい流体力学的インパルスを持つ等しく反対の渦対を形成する。

コメント